MATLAB в инженерных и научных расчетах
Отметим, что эпюры прогибов EIJ(x)
3.3.3. Определение частот собственных колебаний
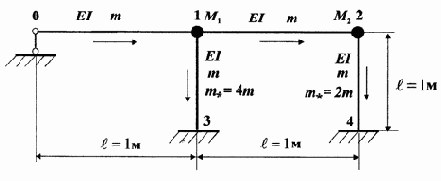 |
Рис. 3.16
Узлы рамы по рис. 3.16 при свободных колебаниях будут иметь линейные и угловые перемещения, т. е. данная конструкция относится к классу свободных систем. При ее движении возникают силы инерции линейно подвижных стержней 0-1 и 1-2. Учет этих сил инерции можно выполнить по формуле [2]

где J(х) – прогиб несвободного стержня, связанного с линейно подвижным стержнем; М – сосредоточенная масса линейно подвижного стержня; а – координата сосредоточенной массы.
В узле 1 прикладываем сосредоточенную массу стержня 0-1 и половину массы стержня 1-2, в итоге получится


Для стержней 1-3 и 2-4 принимаем, что прогиб приближенно описывается функцией


В дальнейшем, при динамическом анализе данной рамы, необходимо использовать увеличенные массы стержней 1-3 и 2-4, чтобы учесть возникающие силы инерции.
Частоты собственных колебаний рамы определяются из частотного уравнения краевой задачи ê А*(w) ê= 0, где матрица А*(w) берется из уравнения (3.28), где достаточно заменить фундаментальные функции статического изгиба на фундаментальные функции поперечных колебаний (3.14).
| 0-1 |
А*=
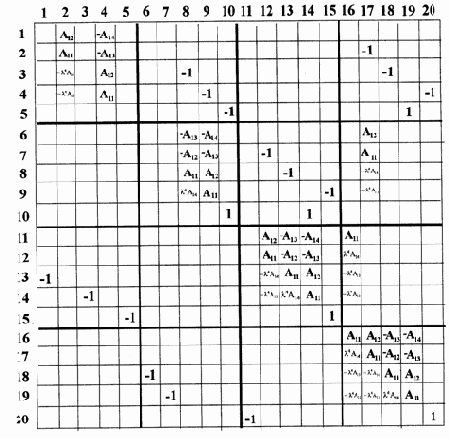

| стержни 0-1; 1-2 | |||||
 | |||||
| стержень 1-3 | (3.31) | ||||
 | |||||
| стержень 2-4 | |||||
 |
/p> где w - частота собственных колебаний. Программа поиска частот принимает вид (обозначения переменных такие же как у неразрезной балки)
п = 20; п1 = 300; am = 0.01; dam = 0.01; X = zeros (n1,1); Y = zeros (n1,1);
for m = 1 : n1
a = zeros (n,n); la1 = sqrt (am); la2 = sqrt
(am); la3 = (2*am^2)^0.25;
la4 = (4*am^2)^0.25;
a(1,2) = (sinh (la1)+
sin(la1))/(2*la1); a(1,4) =-(sinh (la1)- sin(la1))/(2*la1^3);
a(2,2)=(cosh (la1)+cos(la1))/2; a(2,4)=-(cosh(la1)-cos(la1))/(2*la1^2); a(2,17)=-1;
a(3,2) = la1^4*a(2,4); a(3,4) = a(1,2); a(3,8) = - 1; a(3,18) = - 1;
a(4,2) = la1^4*a(2,4); a(4,4) = a(2,2); a(4,9) = - 1; a(4,20) = - 1; a(5,10) = - 1;
a(5,19) = 1; a(6,8) = - (cosh(la2) - cos(la2))/(2*la2^2);
a(6,9)=-(sinh(la2)-sin(la2))/(2*la2^3); a(6,17)=(sinh(la2)+sin(la2))/(2*la2);
a(7,8) =- a(6,17); a(7,9) =
a(6,8); a(7,12) = - 1; a(7,17)=(cosh(la2)+cos(la2))/2;
a(8,8) = a(7,17); a(8,9) =
a(6,17); a(8,13) = - 1; a(8,17) = la2^4*a(6,9);
a(9,8) =- a(8,17); a(9,9) = a(7,17);
a(9,15) = - 1; a(9,17) = la2^4*a(6,8);
a(10,10) = 1; a(10,14) = 1; a(11,12)=(sinh(la3)+sin(la3))/(2*la3);
a(11,13)=-(cosh(la3)-cos(la3))/(2*la3^2); a(11,14)=-(sinh(la3)-sin(la3))/(2*la3^3);
a(11,16)=(cosh(la3)+cos(la3))/2; a(12,12) = a(11,16); a(12,13) =- a(11,12);
a(12,14)=a(11,13); a(12,16)=- la3^4*a(11,14); a(13,1)=-1; a(13,12)=- a(12,16);
a(13,13)=a(12,12); a(13,14)=a(11,12); a(13,16)= la3^4*a(11,13); a(13,1)=-1;
a(14,12)=a(13,16); a(14,13)=-a(13,12); a(14,14)=a(12,12); a(14,15)=-la3^4*a(12,13);
a(15,5) = - 1;
a(15,15) = 1; a(16,16)=(cosh(la4)+cos(la4))/2;
a(16,17)=(sinh(la4)+sin(la4))/(2*la4); a(16,18)=-(cosh(la4)-cos(la4))/(2*la4^2);
a(16,19)=-(sinh(la4)-sin(la4))/(2*la4^3); a(17,16)=- la4^4*a(16,19);
a(17,17)=a(16,16); a(17,18)=-a(16,17); a(17,19)=a(16,18); a(18,6) = - 1;
a(18,16)= la4^4*a(16,18); ); a(18,17)=-a(17,16);
a(18,18)=a(16,16);
a(18,19)=a(16,17); a(19,7) = - 1; a(19,16)=- la4^4*a(16,17);
a(19,17)=a(18,16);
a(19,18)=a(17,16); a(19,19)=a(16,16); a(20,11) = - 1;
a(20,20) = 1; d = det(a); X(m,1) = am; Y(m,1) = d; am = am + dam; end;
plot (X,Y); grid оn
format long e
[X Y]
