MATLAB в инженерных и научных расчетах
Пример подготовки и решения конкретной задачи
Решение любой задачи в системе Simulink должно начинаться с постановки задачи. Чем глубже продумана постановка задачи, тем больше вероятность успешного ее решения. В ходе постановки задачи нужно оценить, насколько решение задачи отвечает возможностям пакета Simulink и какие компоненты последнего могут потребоваться для решения заданной задачи.
В качестве примера рассмотрим тривиальную задачу моделирования работы линейного осциллятора. Осциллятором в механике называют механическую систему с одной степенью свободы, совершающую колебания около положения устойчивого равновесия (например, маятник, груз на пружине). Колебания осциллятора описываются следующим дифференциальным уравнением [ 8 ]

здесь




Данное уравнение применяется также и для исследования колебаний немеханических систем. В частности, колебательный контур является осциллятором. Колебания напряжённостей электрического и магнитного полей в плоской электромагнитной волне вполне можно описывать предыдущим дифференциальным уравнением. В квантовой механике задача о линейном осцилляторе решается с помощью уравнения Шредингера. Законы колебаний линейного осциллятора играют важную роль в теории твёрдого тела, электромагнитного излучения, колебательных спектров молекул.
Запишем уравнение (1) в форме

В основу воплощения уравнения (1) в блок-схему положим следующую идею последовательного итерационного процесса:
- если сформировать правую часть уравнения (1) зависящую от х , x' , считая их известными, то станет известно ускорение x'' осциллятора. Проинтегрировав ускорение, можно получить скорость x' , а последующее интегрирование даёт закон изменения перемещения осциллятора х ( t ). Полученные значения скорости и перемещения можно теперь использовать для формирования правой части.
Итак, для формирования блок-схемы, осуществляющей численное интегрирование, можно сделать следующее:
1. В основу блок-схемы положено два последовательно соединённых интегратора (блоки Integrator) с внешне задаваемыми начальными условиями в соответствии с системой дифференциальных уравнений

и начальными условиями при t = 0 x = x0 , x' = x'0 .
На вход первого интегратора подаётся ускорение V' , а в качестве начального условия используется начальное значение скорости V(0) = x'0 ; выходом этого блока будет текущая скорость осциллятора V = V ( t ); эту величину следует подать на вход второго интегратора с начальным условием в виде начального значения отклонения x (0) = x0 ; выход из блока будет представлять собой искомый закон движения х = х (t).
2. Сформулировать отдельным блоком в виде подмодели (блок Subsystem) функцию правой части f(t, x, x') = h sin (pt) – 2nx' – k2 x , используя в качестве входных параметров полученные значения х ( t ) и x' ( t ) в качестве входных величин - h, p, n, k .
3. Используя созданную подмодель, в основной модели связать сформулированные текущие значения х ( t ) и х' ( t ) с соответствующими входами подмодели, а выход подмодели связать с сумматором; сигнал с выхода сумматора подать на вход первого интегратора, замыкая цепь интегрирования.
4. Для отображения результатов интегрирования в графической форме подсоединить блок Scope к выходу системы – сформированному сигналу х ( t ); для отображения фазового портрета осциллятора использовать блок XY Graph , на входы которого направить сигналы x ( t ) и x' ( t ).
Блок-схема, реализующая указанные идеи приведена на рисунке 4.17.
Отметим также, что при построении блок-схемы подсистемы (рисунке 4.16) связь подсистемы с основной системой осуществляется путём ввода в подсистему стандартных блоков типа In
(Вход) и Out (Выход). Все величины, которые формируются в основной модели, а затем должны быть использованы в подмодели, должны "проникать" в подсистему через блоки In , а величины, сформированные в подсистеме и затем используемые в основной системе, должны "выходить" из подсистемы через блоки Out .
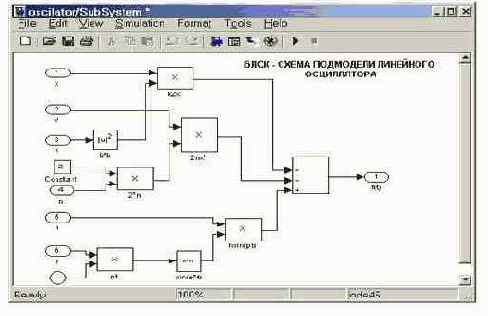
Рис. 4.16. Блок-схема подмодели линейного осциллятора.
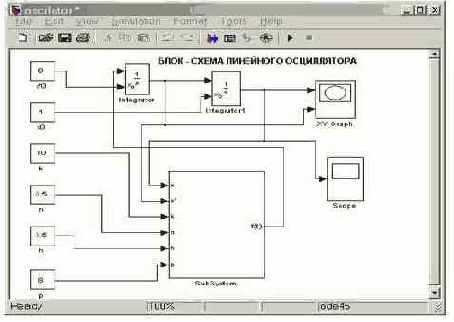
Рис. 4.17. Блок-схема основной модели линейного осциллятора
При этом на изображении блока подсистемы в блок-схеме основной модели автоматически появляется такое количество входов, которое совпадает с числом введенных в подсистеме блоков In , и выходов, равных числу блоков Out , использованных в подсистеме.
Вызвав команду Start из меню Simulation окна основной блок-схемы, можно активизировать процесс моделирования созданной S – модели осциллятора. По окончании этого процесса появится дополнительное графическое окно, созданное блоком XY Graph , на котором изображается фазовый портрет осциллятора при выбранных параметрах. Если теперь дважды щёлкнуть мышью на блоке Scope в блок-схеме осциллятора, то появится ещё одно графическое окно (рисунок 4.18) с графиком зависимости координаты х от времени.
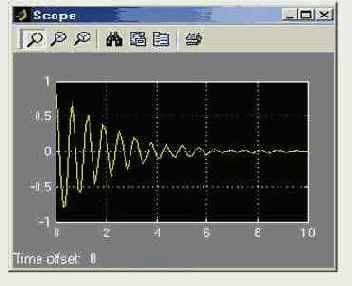
Рис. 4.18. Колебания линейного осциллятора
Изменяя данные настройки входных блоков Constant, можно проводить исследования поведения осциллятора при произвольных значениях входных параметров.
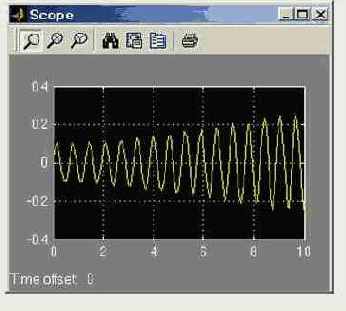
Рис. 4.19. Резонансные колебания осциллятора ( при p = k )
В качестве заданий применения пакета расширений Simulink рассматривается задача об определении управляющих факторов, обеспечивающих программное движение манипулятора [ 7 ].
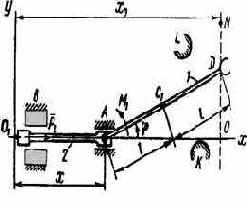
Манипулятор (рис. 4.24 – 4.26), состоящий из звеньев 1, 2 и захвата D, приводится в движение приводами А и В. Захват D перемещается вдоль прямой ON. Co стороны привода А к звену 1 прикладывается либо управляющий момент МА (варианты 2, 4, 7, 8, 12, 22, 24-26, 29), либо управляющее усилие РА (варианты 1, 3, 5, 6, 9-11, 13-21, 23, 27, 28, 30). Привод В воздействует на звено 2 либо моментом МВ (варианты 1-3, 5, 6, 8-11, 13-21, 23, 27), либо управляющим усилием РВ (варианты 4, 7, 12, 22, 24-26, 28-30).
Перемещение звена 1 (варианты 3, 4, 7, 12, 22, 24-26, 28-30) или звена 2 (варианты 1, 2, 5, 6, 8-11, 13 - 21, 23, 27) манипулятора ограничено препятствиями К и L, поэтому изменение угла поворота ? = ? (t) этого звена возможно лишь в интервале [?(0), ?(?)], где ? — время движения звена. Технические условия работы манипулятора требуют, чтобы указанное звено сошло со связи К при t = 0 и «мягко» коснулось препятствия L при t = ?, т. е. так, чтобы были удовлетворены условия

Программные движения звена 1, удовлетворяющие требованиям «мягкого» касания, приняты в таком виде:
1) ? (t) = ? (0) + [? (?) - ? (0)] (10 – 15 t / ? + 6 t2 / ?2) (варианты 2, 4, 6, 7, 11, 12, 16, 19, 22, 24-26, 28-30);
2) ? (t) = ? (0) + [? (?) - ? (0)] [t / ? - (1/(2?)) sin (2?t/?)] (варианты 1, 3, 5, 8-10, 13-15, 17, 18, 20, 21, 23, 27).
Значения ? (0) и ? (?) заданы в таблице. Силами сопротивления движению пренебречь. Механизм расположен в горизонтальной плоскости. Движением захвата относительно звена 1 пренебречь.
В задании приняты следующие обозначения:
m1 — масса первого звена, захвата и переносимого в захвате объекта;
ш2
— масса второго звена;
J1 - момент инерции звена 1, захвата и переносимого в захвате объекта относительно
главной центральной оси инерции;
J2
- момент инерции звена 2.
Центр тяжести звена 1 находится в точке С (варианты 1- 4, 6-8, 11-13, 16, 18-20, 22-30) или в точке А (варианты 5, 9, 10, 14, 15, 17, 21).
Требуется:
1. Вычислить значения управляющих сил и моментов в начале торможения звена 1. Считать, что торможение звена 1 начинается в тот момент, когда угловое ускорение звена обращается в ноль.
2. Построить графики зависимости управляющих моментов и сил от времени.
Пример выполнения задания. Дано: m1 = 2 кг; m2 = 3 кг; Jl = 0,8 кг м2; l = 1 м;
? (0) = 0, ? (?) = ? / 6 рад; ? = 0,5 с.
Центр тяжести звена 1 находится в точке С (рис. 4.20):
? (t) = ? (0) + [? (?) - ? (0)] [t / ? - (1/(2?)) sin
(2?t/?)]
 |
Найти управляющий момент М и управляющую силу Р.
Р е ш е н и е. Для решения задачи применим уравнения Лагранжа II
рода. Будем рассматривать механическую систему как систему с двумя степенями свободы, приняв за обобщенные координаты угол ? поворота звена 1 и смещение х звена 2 (рис.4.20)
Рис. 4.20
Для рассматриваемой механической системы можно записать:
yC2 = const; xC1= х + l cos ? ; yC1
= l sin ? . (1)
Эти равенства играют роль уравнений связей.
В соответствии с выбранными обобщенными координатами имеем

Совокупность уравнений (1) и (2) позволяет составить дифференциальные уравнения движения механической системы.
Составим выражение для кинетической энергии системы Т как функцию обобщенных скоростей



Кинетическая энергия звена 1, совершающего плоское движение,

где


Продифференцировав (1) по времени, будем иметь


откуда

Таким образом,


Определим обобщенные силы Q? и Qx .
Обобщенные силы Qx
и Q? можно определить и из выражения работы сил на элементарных перемещениях системы, соответствующих вариации каждой обобщенной координаты:
?Ax=Qx?x = P ?x; ?A?=Q??? = M ?? ,
отсюда Qx = Р и Q? = М .
Подставляя полученные значения кинетической энергии и обобщённых сил в уравнения Лагранжа II
рода (2), получим


Эти равенства представляют собой зависимость управляющего момента М и управляющего усилия Р от известных функций

Данные управляющие факторы находим с помощью пакета расширения Simulink , составляя блочную модель механизма манипулятора
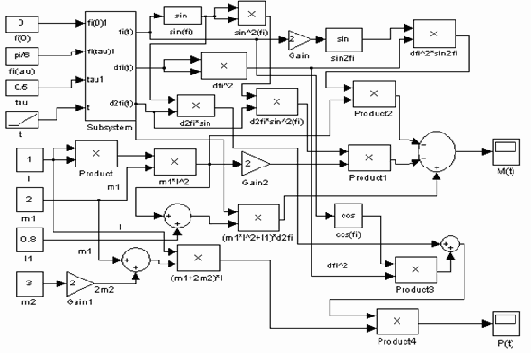
Рис. 4.21. Модель механизма манипулятора
Данная модель содержит подмодель (рис. 4.22), определяющая изменение

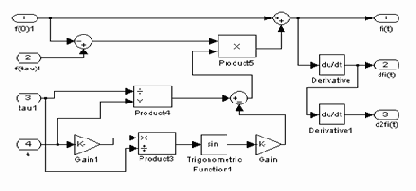
Рис. 4.22. Субмодель механизма манипулятора
Результат такого имитационного моделирования для управляющих факторов представляется в виде двух осциллограмм
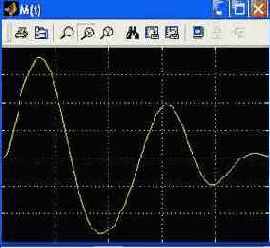
Рис. 4.23, a. Программное изменение управляющего момента M (t)
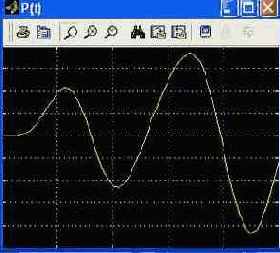
Рис. 4.23, b. Программное изменение управляющего усилия Р (t)
Варианты расчётов управляющих моментов М (t) и сил Р (t) , обеспечивающих программное движение манипулятора приведены на рисунках 4.24 – 4.26, соответствующие числовые данные приведены в таблице.
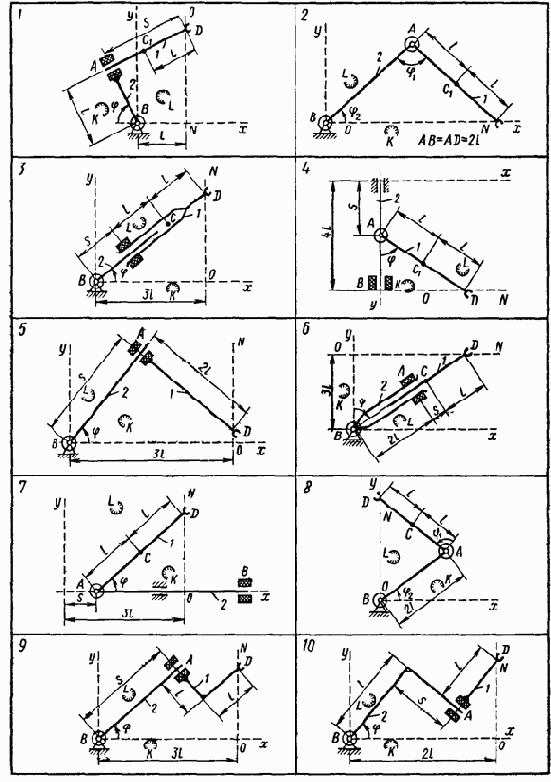
Рис. 4.24
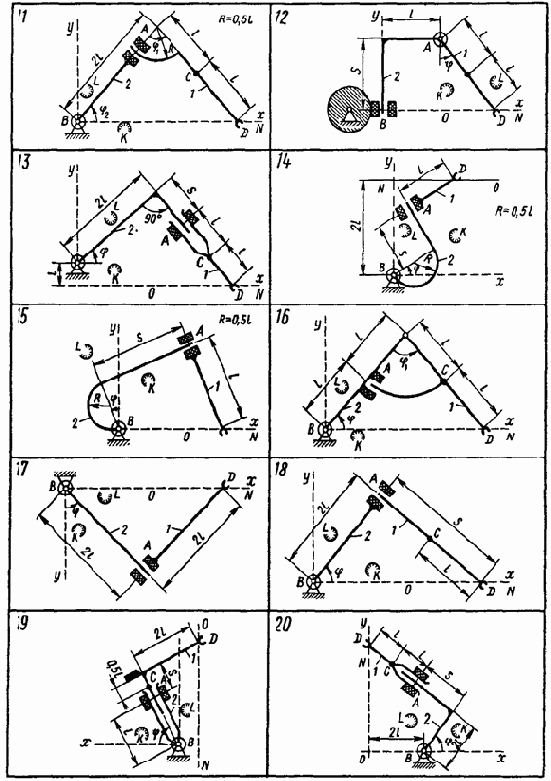
Рис. 4.25
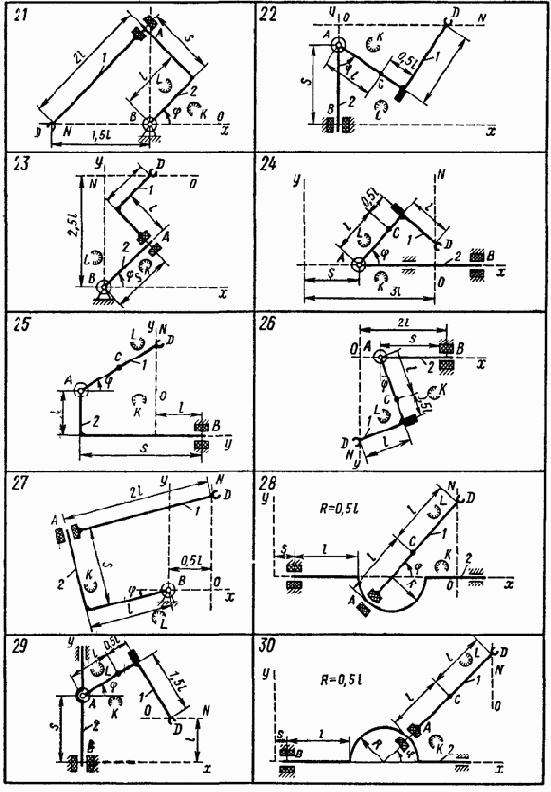
Рис. 4.26
|
Номер варианта |
m1 |
m2 |
J1 |
J2 |
l, м |
?, с |
?(0) |
?(?) |
|
кг |
кг |
кг м2 |
кг м2 |
рад |
рад |
|||
|
1 |
3 |
- |
0,5 |
0,6 |
0,5 |
1 |
? / 3 |
2 ? / 3 |
|
2 |
4 |
- |
1 |
2 |
0,3 |
0,25 |
0 |
?/3 |
|
3 |
2 |
- |
1 |
2 |
0,2 |
1 |
0 |
?/3 |
|
4 |
2,5 |
2,5 |
0,8 |
- |
0,8 |
0,5 |
?/6 |
?/3 |
|
5 |
4 |
- |
2 |
2 |
0,5 |
2 |
?/6 |
?/3 |
|
6 |
2,5 |
- |
1,2 |
1,5 |
0,3 |
0,9 |
0 |
?/3 |
|
7 |
2 |
3 |
0,6 |
- |
0,7 |
0,5 |
?/6 |
?/3 |
|
8 |
3 |
- |
0,9 |
2 |
0,4 |
0,3 |
?/6 |
?/3 |
|
9 |
2 |
- |
0,8 |
1,4 |
0,3 |
1 |
0 |
?/3 |
|
10 |
3,5 |
- |
1,4 |
1,6 |
0,4 |
2 |
0 |
?/6 |
|
11 |
2,5 |
- |
1 |
1,4 |
0,5 |
0,5 |
0 |
?/4 |
|
12 |
3 |
3 |
0,7 |
- |
0,7 |
0,4 |
?/6 |
?/3 |
|
13 |
4 |
- |
1,5 |
2 |
0,3 |
0,5 |
0 |
?/6 |
|
14 |
3 |
- |
1,4 |
1,8 |
0,4 |
1,5 |
?/6 |
?/3 |
|
15 |
2,5 |
- |
1 |
1,2 |
0,5 |
0,5 |
?/6 |
?/3 |
|
16 |
3 |
- |
1,2 |
2 |
0,3 |
0,3 |
0 |
?/4 |
|
17 |
3 |
- |
1,2 |
2 |
0,3 |
1,8 |
?/6 |
?/3 |
|
18 |
2 |
- |
0,6 |
0,8 |
0,4 |
0,8 |
?/6 |
?/3 |
|
19 |
3 |
- |
1,7 |
2 |
0,3 |
0,6 |
?/6 |
?/3 |
|
20 |
3,5 |
- |
1,2 |
1,6 |
0,4 |
0,6 |
?/4 |
?/2 |
|
21 |
4 |
- |
2 |
2 |
0,5 |
0,5 |
?/6 |
?/4 |
|
22 |
2,5 |
4 |
1,2 |
1,8 |
0,3 |
0,8 |
?/6 |
?/2 |
|
23 |
4 |
- |
1,1 |
1,7 |
0,4 |
1 |
?/3 |
?/2 |
|
24 |
3 |
3 |
1,4 |
- |
0,6 |
1 |
0 |
?/3 |
|
25 |
2,5 |
3 |
1 |
- |
0,8 |
0,5 |
0 |
?/3 |
|
26 |
3,5 |
4 |
1,6 |
2 |
0,4 |
0,9 |
0 |
?/6 |
|
27 |
2 |
- |
1,1 |
1,5 |
0,4 |
0,7 |
0 |
?/3 |
|
28 |
3 |
2,5 |
0,7 |
- |
0,7 |
0,4 |
?/6 |
?/3 |
|
29 |
2 |
3 |
1,3 |
- |
0,5 |
1,2 |
0 |
?/3 |
|
30 |
2,5 |
4 |
0,8 |
0,6 |
0,4 |
?/6 |
?/4 |
