MATLAB в инженерных и научных расчетах
Для построения эпюр программируем выражения
|
№ п/п |
Граничные параметры |
|
1 |
 |
|
2 |
 |
|
3 |
 |
|
4 |
 |
|
5 |
 |
|
6 |
 |
|
7 |
 |
|
8 |
 |
|
9 |
 |
|
10 |
 |
|
11 |
 |
|
12 |
 0.8570 кНм2 |
|
13 |
 |
|
14 |
 |
|
15 |
 |
|
16 |
 |
|
17 |
 1.7751 кНм2 |
|
18 |
 |
|
19 |
 |
|
20 |
 |
3.3.2. Построение эпюр напряженно-деформированного состояния
элементов рамы
Для построения эпюр программируем выражения (3.12), (3.13)
стержень 0-1
х = 0 : 0.001 : 1.0; q = 10.0;
EIv = - (X(2,1)*x - X(4,1)*x.^ 3 / 6 + q*x.^4 / 24);
EIfi
= - (X(2,1) - X(4,1)*x.^ 2 / 2 + q*x.^3 / 6);
Q = X(4,1) - q*x; M = X(4,1)*x - q*x.^ 2 / 2;
subplot (2,2,1), plot (x, EIv); axis
([0 1 - 0.4 0.4]); grid on
subplot (2,2,2), plot (x, EIfi); axis ([0 1 - 2 2]); grid on
subplot (2,2,3), plot (x, Q); axis
([0 1 - 10 10]); grid on
subplot (2,2,4), plot (x, M); axis
([0 1 - 5 5 ]); grid on
стержень 1-2
х = 0 : 0.001 : 1.0; q = 10.0;
EIv = - (X(17,1)*x - X(8,1)*x.^ 2 / 2- X(9,1)*x.^ 3 / 6 + q*x.^4 / 24);
EIfi
= - (X(17,1) - X(8,1)*x- X(9,1)*x.^ 2 / 2 + q*x.^3 / 6);
Q = X(9,1) - q*x; M = X(8,1) + X(9,1)*x - q*x.^ 2 / 2;
subplot (2,2,1), plot (x, EIv); axis
([0 1 - 0.4 0.4]); grid on
subplot (2,2,2), plot (x, EIfi); axis ([0 1 - 2 2]); grid on
subplot (2,2,3), plot (x, Q); axis
([0 1 - 22 22]); grid on
subplot (2,2,4), plot (x, M); axis
([0 1 - 10 10]); grid on
стержень 1-3
а). интервал (0;

х = 0 : 0.001 : 0.75;
EIv = - (X(16,1) + X(17,1)*x- X(18,1)*x.^
2 / 2 - X(19,1)*x.^
3 / 6);
EIfi
= - (X(17,1) - X(18,1)*x- X(19,1)*x.^ 2 / 2);
Q = X(19,1); M = X(18,1) + X(19,1)*x;
subplot (2,2,1), plot (x, EIv); axis
([0 0.25 - 3 3]); grid on
subplot (2,2,2), plot (x, EIfi); axis ([0 0.25 - 6 6]); grid on
subplot (2,2,3), plot (x, Q); axis
([0 0.25 - 2 2]); grid on
subplot (2,2,4), plot (x, M); axis
([0 0.25 - 14 14]); grid on
б). интервал (


х = 0.25 : 0.001 : 1.0; m = 20.0;
EIv=-(X(16,1)+X(17,1)*x-X(18,1)*x.^ 2/2-X(19,1)*x.^ 3/6+m*(x-0.25).^ 2/2);
EIfi
= - (X(17,1) - X(18,1)*x- X(19,1)*x.^ 2 / 2+m*(x-0.25));
Q = X(19,1); M = X(18,1) + X(19,1)*x - m;
subplot (2,2,1), plot (x, EIv); axis
([0.25 1.0 - 3 3]); grid on
subplot (2,2,2), plot (x, EIfi); axis ([0.25 1.0 - 6 6]); grid on
subplot (2,2,3), plot (x, Q); axis
([0.25 1.0 - 2 2]); grid on
subplot (2,2,4), plot (x, M); axis
([0.25 1.0 - 15 15]); grid on
стержень 2-4
а). интервал (0;

х = 0 : 0.001 : 0.5;
EIv = - (X(16,1) + X(12,1)*x- X(13,1)*x.^
2 / 2 - X(14,1)*x.^
3 / 6);
EIfi
= - (X(12,1) - X(13,1)*x- X(14,1)*x.^ 2 / 2);
Q = X(14,1); M = X(13,1) + X(14,1)*x;
subplot (2,2,1), plot (x, EIv); axis
([0 0.5 - 3 3]); grid on
subplot (2,2,2), plot (x, EIfi); axis ([0 0.5 - 6 6]); grid on
subplot (2,2,3), plot (x, Q); axis
([0 0.5 - 2 2]); grid on
subplot (2,2,4), plot (x, M); axis
([0 0.5 - 15 15]); grid on
б). интервал (


х = 0.5 : 0.001 : 1.0; f = 60.0;
EIv=-(X(16,1)+X(12,1)*x-X(13,1)*x.^ 2/2-X(14,1)*x.^ 3/6+ f *(x-0.5).^ 3/6);
EIfi
= - (X(12,1) - X(13,1)*x- X(14,1)*x.^ 2 / 2+ f *(x-0.5).^ 2/2);
Q = X(14,1) - f; M = X(13,1) + X(14,1)*x - f *(x-0.5);
subplot (2,2,1), plot (x, EIv); axis
([0.5 1.0 - 3 3]); grid on
subplot (2,2,2), plot (x, EIfi); axis ([0.5 1.0 - 6 6]); grid on
subplot (2,2,3), plot (x, Q); axis
([0.5 1.0 - 60 60]); grid on
subplot (2,2,4), plot (x, M); axis
([0.5 1.0 - 25 25]); grid on
Эпюры прогибов EIJ(x), углов поворота EIj(x), поперечных сил Q(x) и изгибающих моментов М(x) представлены на рис. 3.15
|
а) |
b) |
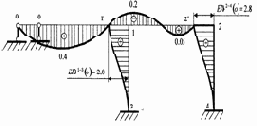 |
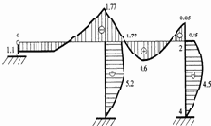 |
|
EIJ(x) кНм3 |
EIj(x) кНм2 |
|
с) |
d) |
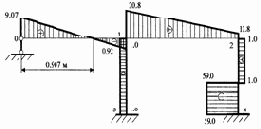 |
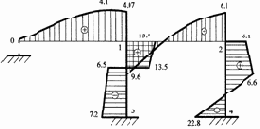 |
|
Q(x) к |
М(x) кНм |
|
Рис. 3.15 |
