Понятие о методе фазового пространства
Для описания поведения систем весьма удобным является метод фазового пространства или, в другой терминологии, - метод пространства состояний. Параметры состояния системы при этом носят название фазовых координат системы. Состояние системы в каждый момент времени может быть изображено точкой в многомерном пространстве, где по координатным осям отложены значения соответствующих фазовых координат.
Если состояние системы изменяется во времени, то изображающая ее точка перемещается в многомерном фазовом пространстве по некоторой кривой, которая называется фазовой траекторией системы. Таким образом, описание поведения системы, часто весьма сложного можно заменить описанием поведения точки в многомерном признаковом пространстве.
В реальных системах фазовые координаты, как правило, могут принимать значения, лежащие в определенных интервалах






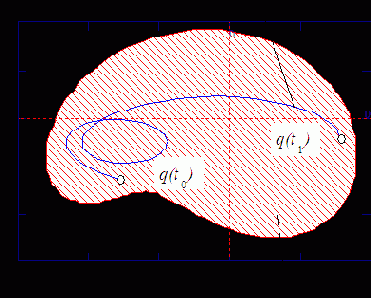 |
Если фазовые координаты системы могут принимать в пределах области существования любые значения, то такая система называется непрерывной. Если фазовые координаты могут принимать только конечное число фиксированных значений, то система называется дискретной.
Очевидно, помимо фазового пространства состояний могут быть построены фазовые пространства входа и выхода. Тогда можно говорить о том, что перемещению динамической системы в фазовом пространстве входа будут соответствовать некоторые перемещения в фазовом пространстве состояний и фазовом пространстве выхода, то есть существует некоторое отображение, связывающая поведение системы в фазовых пространствах входа, состояний и выхода.
