Свойства мультипликативных зависимостей
Для того чтобы представить характер функциональных связей между основными характеристиками процесса резания, рассмотрим основные свойства мультипликативных зависимостей, которые используются для их описания.
Простейшей формой мультипликативной (степенной) зависимости является двумерная степенная зависимость

Очевидно, именно такой зависимостью описывается связь между характеристиками процесса резания и каждым из технологических параметров в формулах (10.2)-(10.4). Таким образом, поняв, что из себя представляет функция (10.5), мы сможем понять основной характер связи между технологическими параметрами и определить область применимости мультипликативных моделей. На рисунке 10.1 приведены графики, которые иллюстрируют поведение степенной функции при различных значениях параметра

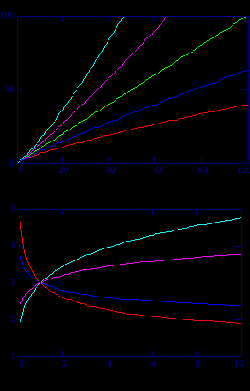 Рис 10.1. Общий вид степенной функции  |
Анализируя графики на рисунке 10.1, мы можем сделать следующие выводы.
1. При значении параметра





2. В случае если

3. В случае если



4. Степенные функции не имеют точек перегиба.
Таким образом, степенные зависимости не могут использоваться в тех случаях, когда для адекватного описания процессов резания требуются функции, имеющие точки экстремума и перегиба (например, при описании зависимости степени усадки стружки от скорости резания или суммарного периода стойкости от времени работы между переточками).
