Гипотеза о законе возрастания эмерджентности и следствия из него
Численные расчеты и аналитические выкладки в соответствии с СТИ показывают, что при возрастании количества элементов в системе доля системной информации в поведении ее элементов возрастает. Это обнаруженное нами новое фундаментальное свойство систем предлагается назвать законом возрастания эмерджентности.
Закон возрастания эмерджентности: "Чем больше элементов в системе, тем большую долю содержащейся в ней информации составляет информация, содержащаяся во взаимосвязях ее элементов".
На рисунках 26 и 27 приведены графики скорости и ускорения возрастания эмерджентности в зависимости от количества элементов W в системе.
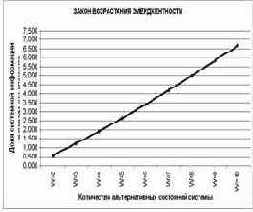 | 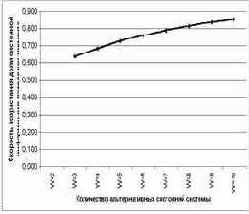 | ||
| Рисунок 26. Возрастание доли системной информации в поведении элемента системы при увеличении количества элементов W | Рисунок 27. Ускорение возрастания доли системной информации в поведении элемента системы от количества элементов W |
Более детальный анализ предполагаемого закона возрастания эмерджентности с использованием конечных разностей первого и второго порядка (таблица 11) показывает, что при увеличении количества элементов в системе доля системной информации в ней возрастает с ускорением, которое постепенно уменьшается. Это утверждение будем называть леммой 1.
Продолжим анализ закона возрастания эмерджентности. Учитывая, что:
 |
выражение (3.3) принимает вид:
 | (3. 13) |
где: 1<=М<=W.
 |
и учитывая, что Log21=0, выражение (3.13) приобретает вид:
 | (3. 14) |
Где введены обозначения:
 | (3. 15) |
С учетом (3.14) выражение (3.9) для коэффициента эмерджентности Хартли приобретает вид:
 |
Заменяя в (3.13) факториал на Гамма-функцию, получаем обобщение выражения (3.3) на непрерывный случай:
 |
Или окончательно:
 | (3. 16) |
Для непрерывного случая обозначения (3.15) принимают вид:
 | (3. 17) |
Учитывая выражения (3.9) и (3.16) получим выражение для коэффициента эмерджентности Хартли для непрерывного случая:
 |
И окончательно для непрерывного случая:
 | (3. 18) |
