Математическая модель СК-анализа

Системное обобщение формулы Хартли

В выражении (3) приведено системное обобщение формулы Хартли для равновероятных состояний объекта управления.

		(1)				(4)
		(2)				(5)
		(3)		с очень малой и быстро уменьшающейся погрешностью		(6)

W – количество чистых (классических) состояний системы.

j – коэффициент эмерджентности Хартли (уровень системной организации объекта, имеющего W чистых состояний).

Гипотеза о Законе возрастания эмерджентности

Исследование математических выражений системной теории информации (7 – 12) позволило сформулировать гипотезу о существовании "Закона возрастания эмерджентности". Суть этой гипотезы в том, что в самих элементах системы содержится сравнительно небольшая доля всей содержащейся в ней информации, а основной ее объем составляет системная информация, содержащаяся в подсистемах различного уровня иерархии.

Различие между классическим и предложенным системным понятиями информации соответствует различию между понятиями МНОЖЕСТВА И СИСТЕМЫ, на основе которых они сформированы.

		(7)				(8)
		(9)				(10)
		(11)				(12)

Математическая формулировка:

Интерпретация

Системное обобщение формулы Харкевича

Ниже приведен вывод системного обобщения формулы Харкевича, а именно:

– классическая формула Харкевича через вероятности перехода системы в целевое состояние при условии сообщения ей определенной информации и самопроизвольно (13);

– выражение классической формулы Харкевича через частоты (14, 15);

– вывод коэффициента эмерджентности Харкевича на основе принципа соответствия с выражением Хартли в детерминистском случае (16 –19);

– вывод системного обобщения формулы Харкевича;

– окончательное выражение для системного обобщения формулы Харкевича (21).

Классическая формула Харкевича

(13)

Pij – вероятность перехода объекта управления в j-е состояние в условиях действия i-го фактора;

Pj – вероятность самопроизвольного перехода объекта управления в j-е состояние, т.е.
в условиях отсутствия действия i-го фактора или всреднем.

Известно, что корреляция не является мерой причинно-следственных связей. Если корреляция между действием некоторого фактора и переходом объекта управления в определенное состояние высока, то это еще не значит, что данный фактор является причиной этого перехода. Для того чтобы по корреляции можно было судить о наличии причинно-следственной связи необходимо сравнить исследуемую группу с контрольной группой, т.е. с группой, в которой данный фактор не действовал.

Также и высокая вероятность перехода объекта управления в определенное состояние в условиях действия некоторого фактора сама по себе не говорит о наличии причинно-следственной связи между ними, т.е. о том, что данный фактор обусловил переход объекта в это состояние. Это связано с тем, что вероятность перехода объекта в это состояние может быть вообще очень высокой независимо от действия фактора. Поэтому в качестве меры силы причинной обусловленности определенного состояния объекта действием некоторого фактора Харкевич предложил логарифм отношения вероятностей перехода в объекта в это состояние в условиях действия фактора и при его отсутствии или в среднем (13).

Таким образом семантическая мера информации Харкевича является мерой наличия причинно-следственных связей между факторами и состояниями объекта управления.

Выражение классической формулы Харкевича через частоты фактов

(14)

(15)

Вывод коэффициента эмерджентности Харкевича на основе принципа соответствия с выражением Хартли в детерминистском случае

Однако мера Харкевича (13) не удовлетворяет принципу соответствия мерой Хартли как мера Шеннона, т.е. не переходит в меру Хартли в детерминистском случае, т.е. когда каждому будущему состоянию объекта управления соответствует единственный уникальный фактор и между факторами и состояниями имеется взаимно однозначное соответствие (17).

(16)

(17)

Откуда:

(18)

(19)

Вывод системного обобщения формулы Харкевича

(20)

Окончательное выражение для системного обобщения формулы Харкевича

(21)

Связь системной теории информации (СТИ) с теорией Хартли-Найквиста-Больцмана и теорией Шеннона

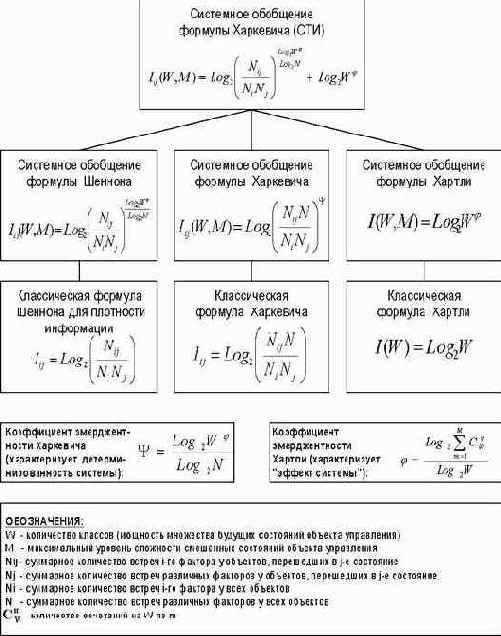
Связь между выражениями для плотности информации в теориях Хартли, Шеннона и СТИ приведена на рисунке 41.

Рисунок 41. Связь между выражениями для плотности информации в теориях Хартли, Шеннона и СТИ

Интерпретация коэффициентов эмерджентности СТИ

Интерпретация коэффициентов эмерджентности, предложенных в рамках системной теории информации, приведена на рисунке 42.

Рисунок 42. Интерпретация коэффициентов эмерджентности СТИ

Коэффициент эмерджентности Хартли j (4) представляет собой относительное превышение количества информации о системе при учете системных эффектов (смешанных состояний, иерархической структуры ее подсистем и т.п.) над количеством информации без учета системности, т.е. этот коэффициент является аналитическим выражением для уровня системности объекта.

Коэффициент эмерджентности Харкевича Y, изменяется от 0 до 1 и определяет степень детерминированности системы.

Таким образом, в предложенном системном обобщении формулы Харкевича (21) впервые непосредственно в аналитическом выражении для самого понятия "Информация" отражены такие фундаментальные свойства систем, как "Уровень системности" и "Степень детерминированности" системы.

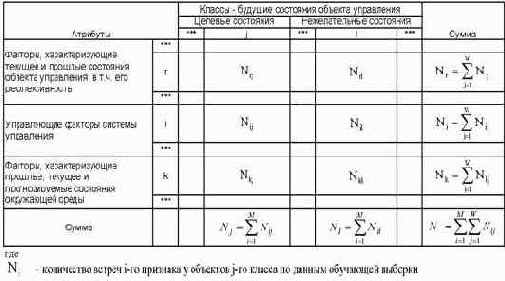
Матрица абсолютных частот

Основной формой первичного обобщения эмпирической информации в модели является матрица абсолютных частот (таблица 23). В этой матрице строки соответствуют факторам, столбцы – будущим целевым и нежелательным состояниям объекта управления, а на их пересечении приведено количество наблюдения фактов (по данным обучающей выборки), когда действовал некоторый i-й фактор и объект управления перешел в некоторое j-е состояние.

Таблица 23 – МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ

Матрица информативностей

Непосредственно на основе матрицы абсолютных частот с использованием системного обобщения формулы Харкевича (21) рассчитывается матрица информативностей (таблица 24).



Таблица 24 – МАТРИЦА ИНФОРМАТИВНОСТЕЙ

Матрица информативностей является универсальной формой представления смысла эмпирических данных в единстве их дискретного и интегрального представления (причины – последствия, факторы – результирующие состояния, признаки – обобщенные образы классов, образное – логическое, дискретное – интегральное).

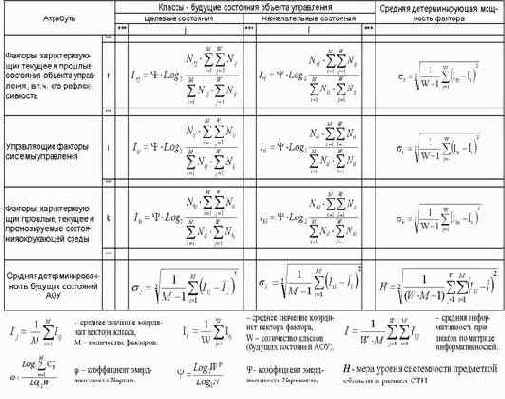Весовые коэффициенты матрицы информативностей непосредственно определяют, какое количество информации Iij система управления получает о наступлении события: "объект управления перейдет в j–е состояние", из сообщения: "на объект управления действует i–й фактор".

Когда количество информации Iij>0 – i–й фактор способствует переходу объекта управления в j–е состояние, когда Iij<0 – препятствует этому переходу, когда же Iij=0 – никак не влияет на это.

Таким образом, предлагаемая семантическая информационная модель позволяет непосредственно на основе эмпирических данных и независимо от предметной области рассчитать, какие количество информации содержится в любом событии о любом другом событии.

Этот вывод является ключевым для данной работы, т.к. конкретно показывает возможность числовой обработки в СК-анализе как числовой, так и нечисловой информации.

Матрица информативностей является также обобщенной (неклассической) таблицей решений, в которой входы (факторы) и выходы (будущие состояния объекта управления) связаны друг с другом не с помощью классических (Аристотелевских) импликаций, принимающих только значения: "Истина" и "Ложь", а различными значениями истинности, выраженными в битах

и принимающими значения от положительного теоретически-максимально-возможного, до теоретически неограниченного отрицательного. Некоторые неклассические высказывания, генерируемые на основе матрицы информативности, приведены на плакате.

Неметрический интегральный критерий сходства, основанный на лемме Неймана-Пирсона

В выражениях (22 – 24) приведен неметрический интегральный критерий сходства, основанный на фундаментальной лемме Неймана-Пирсона, обеспечивающий идентификацию и прогнозирование в предложенных неортонормированных



семантических пространствах с финитной метрикой, в которых в качестве координат векторов будущих состояний объекта управления и факторов выступает количество информации, рассчитанное в соответствии с системной теорией информации (21), а не Булевы координаты или частоты, как обычно.

(22)

(23)

Или в координатной форме:

(24)

(25)

– вектор j–го состояния объекта управления;

 – вектор состояния предметной области, включающий все виды факторов, характеризующих объект управления, возможные управляющие воздействия и окружающую среду (массив–локатор), т.е.:

(26)

(27)

       – средняя информативность по вектору класса;

      – среднее по вектору идентифицируемой ситуации (объекта).

      – среднеквадратичное отклонение информативностей вектора класса;

      – среднеквадратичное отклонение по вектору распознаваемого объекта.

Связь системной меры целесообразности информации с критерием c2

В (28 – 33) показана связь системной меры целесообразности информации с известным критерием c2, а также предложен новый критерий уровня системности предметной области, являющийся нормированным объемом семантического пространства (34, 35).

(28)

(29)

– Nij – фактическое количество встреч i-го признака у объектов j-го класса;

– t    –  ожидаемое количество встреч i-го признака у объектов j-го класса.

	(30)		(31)
	(32)		(33)
	(34)		(35)

Предлагается более точный критерий уровня системности модели является объем неортонормированного семантического пространства, рассчитанный как объем многомерного параллелепипеда, ребрами которого являются оси семантического пространства. Однако для этой меры сложнее в общем виде записать аналитическое выражение и для ее вычисления могут быть использованы численные методы с использованием многомерного обобщения смешанного произведения векторов.

Абстрагирование (ортонормирование) существенно уменьшает размерность семантического пространства без существенного уменьшения его объема.



Оценка адекватности семантической информационной модели в СК-анализе и бутстрепные методы

Под адекватностью модели СК-анализа понимается ее внутренняя и внешняя дифференциальная и интегральная валидность. Понятие валидности является уточнением понятия адекватности, для которого определены процедуры количественного измерения, т.е. валидность – это количественная адекватность. Это понятие количественно отражает способность модели давать правильные результаты идентификации, прогнозирования и способность вырабатывать правильные рекомендации по управлению.

Под внутренней валидностью понимается валидность модели, измеренная после синтеза модели путем идентификации объектов обучающей выборки.

Под внешней валидностью понимается валидность модели, измеренная после синтеза модели путем идентификации объектов, не входящих в обучающую выборку.

Под дифференциальной валидностью модели понимается достоверность идентификации объектов в разрезе по классам.

Под интегральной валидностью средневзвешенная дифференциальная валидность.

Возможны все сочетания: внутренняя дифференциальная валидность, внешняя интегральная валидность и т.д.

Основная идея бутстрепа по Б.Эфрону [110] состоит в том, что методом Монте-Карло (статистических испытаний) многократно извлекаются выборки из эмпирического распределения. Эти выборки, естественно, являются вариантами исходной, напоминают ее.

Эта идея позволяет сконструировать алгоритм измерения адекватности модели, состоящий из двух этапов:

1. Синтез модели на одном случайном подмножестве обучающей выборки.

2. Измерение валидности модели на оставшемся подмножестве обучающей выборки, не использованном для синтеза модели.

Поскольку оба случайных подмножества имеют переменный состав по объектам обучающей выборки, то подобная процедура должна повторяться много раз, после чего могут быть рассчитаны статистические характеристики адекватности модели, например, такие как:

– средняя внешняя валидность;

– среднеквадратичное отклонение текущей внешней валидности от средней и другие.



Достоинство бутстрепного подхода к оценке адекватности модели состоит в том, что он позволяет измерить внешнюю валидность на уже имеющейся выборке и изучить статистические характеристики, характеризующие адекватность модели при изменении объема и состава выборки.

Непараметричность модели. Робастные процедуры и фильтры для исключения артефактов

Предложенная семантическая информационная модель является непараметрической, т.к. базируется на системной теории информации [64], которая никоим образом не основана на предположениях о нормальности распределений исследуемой выборки.

Под робастными понимаются процедуры, обеспечивающие устойчивую работу модели на исходных данных, зашумленных артефактами, т.е. данными, выпадающими из общих статистических закономерностей, которым подчиняется исследуемая выборка.

Критерий выявления артефактов, реализованный в СК-анализе, основан на том, что при увеличении объема статистики частоты значимых атрибутов растут, как правило, пропорционально объему выборки, а частоты артефактов так и остаются чрезвычайно малыми, близкими к единице. Таким образом, выявление артефактов возможно только при достаточно большой статистике, т.к. в противном случае недостаточно информации о поведении частот атрибутов с увеличением объема выборки.

В модели реализована такая процедура удаления наиболее вероятных артефактов, и она, как показывает опыт, существенно повышает качество (адекватность) модели.


Содержание раздела

---

---