Однослойная нейронная сеть и персептрон Розенблата
Исторически первой искусственной нейронной сетью, способной к перцепции (восприятию) и формированию реакции на воспринятый стимул, явился Perceptron
Розенблатта (F.Rosenblatt, 1957). Термин " Perceptron" происходит от латинского perceptio, что означает восприятие, познавание. Русским аналогом этого термина является "Персептрон". Его автором персептрон рассматривался не как конкретное техническое вычислительное устройство, а как модель работы мозга. Современные работы по искусственным нейронным сетям редко преследуют такую цель.
Простейший классический персептрон содержит элементы трех типов (рисунок 75), назначение которых в целом соответствует нейрону рефлекторной нейронной сети, рассмотренному выше.
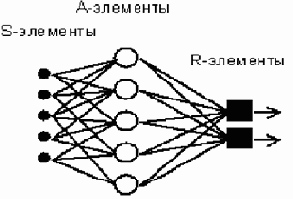 | |
| Рисунок 75. Элементарный персептрон Розенблатта |
S-элементы – это сенсоры или рецепторы, принимающие двоичные
сигналы от внешнего мира. Каждому S-элементу соответствует определенная градация некоторой описательной шкалы.
Далее сигналы поступают в слой ассоциативных или A-элементов (показана часть связей от S к A-элементам). Только ассоциативные элементы, представляющие собой формальные нейроны, выполняют совместную аддитивную
обработку информации, поступающей от ряда S-элементов с учетом изменяемых
весов связей (рисунок 75). Каждому A-элементу соответствует определенная градация некоторой классификационной шкалы.
R-элементы с фиксированными весами формируют сигнал реакции персептрона на входной стимул. R-элементы обобщают информацию о реакциях нейронов на входной объект, например могут выдавать сигнал об идентификации данного объекта, как относящегося к некоторому классу только в том случае, если все нейроны, соответствующие этому классу выдадут результат именно о такой идентификации объекта. Это означает, что в R-элементах может использоваться мультипликативная функция от выходных сигналов нейронов. R-элементы также, как и A-элементы, соответствует определенным градациям классификационных шкал.
Розенблатт считал такую нейронную сеть трехслойной, однако по современной терминологии, представленная сеть является однослойной, так как имеет только один слой нейропроцессорных элементов.
Если бы R- элементы были тождественными по функциям A-элементам, то нейронная сеть классического персептрона была бы двухслойной. Тогда бы A-элементы выступали для R-элементов в роли S-элементов.
Однослойный персептрон характеризуется матрицей синаптических связей ||W|| от S- к A-элементам. Элемент матрицы отвечает связи, ведущей от i-го S-элемента (строки) к j-му A-элементу (столбцы). Эта матрица очень напоминает матрицы абсолютных частот и информативностей, формируемые в семантической информационной модели, основанной на системной теории информации.
С точки зрения современной нейроинформатики однослойный персептрон представляет в основном чисто исторический интерес, вместе с тем на его примере могут быть изучены основные понятия и простые алгоритмы обучения нейронных сетей.
Обучение классической нейронной сети
состоит в подстройке весовых коэффициентов каждого нейрона.
Пусть имеется набор пар векторов {xa, ya}, a = 1..p, называемый обучающей выборкой, состоящей из p объектов.
Вектор {xa} характеризует систему признаков конкретного объекта a обучающей выборки, зафиксированную S-элементами.
Вектор {ya} характеризует картину возбуждения нейронов при предъявлении нейронной сети конкретного объекта a обучающей выборки:
 |
на данной обучающей выборке, если при подаче на вход сети вектора {xa} на выходе всегда получается соответствующий вектор {ya}, т.е. каждому набору признаков соответствуют определенные классы.
Ф.Розенблаттом предложен итерационный алгоритм обучения из 4-х шагов, который состоит в подстройке матрицы весов, последовательно уменьшающей ошибку в выходных векторах:
|
Шаг 0: |
Начальные значения весов всех нейронов полагаются случайными. |
|
Шаг 1: |
Сети предъявляется входной образ xa, в результате формируется выходной образ. |
|
Шаг 2: |
Вычисляется вектор ошибки, делаемой сетью на выходе. |
|
Шаг 3: |
Вектора весовых коэффициентов корректируются таким образом, что величина корректировки пропорциональна ошибке на выходе и равна нулю если ошибка равна нулю: – модифицируются только компоненты матрицы весов, отвечающие ненулевым значениям входов; – знак приращения веса соответствует знаку ошибки, т.е. положительная ошибка (значение выхода меньше требуемого) проводит к усилению связи; – обучение каждого нейрона происходит независимо от обучения остальных нейронов, что соответствует важному с биологической точки зрения, принципу локальности обучения. |
|
Шаг 4: |
Шаги 1-3 повторяются для всех обучающих векторов. Один цикл последовательного предъявления всей выборки называется эпохой. Обучение завершается по истечении нескольких эпох, если выполняется по крайней мере одно из условий: – когда итерации сойдутся, т.е. вектор весов перестает изменяться; – когда полная просуммированная по всем векторам абсолютная ошибка станет меньше некоторого малого значения. |
Данный алгоритм относится к широкому классу алгоритмов обучения с учителем, т.к. в нем считаются известными не только входные вектора, но и значения выходных векторов, т.е. имеется учитель, способный оценить правильность ответа ученика, причем в качестве последнего выступает нейронная сеть.
Розенблаттом доказана "Теорема о сходимости обучения" по d-правилу. Эта теорема говорит о том, что персептрон способен обучится любому обучающему набору, который он способен представить. Но она ничего не говорит о том, какие именно обучающие наборы он способен представить. Ответ на этот вопрос мы получим в следующем разделе.
