Решение задачи "Синтез семантической информационной модели активного объекта управления"
Исходные данные для выявления взаимосвязей между факторами и состояниями объекта управления предлагается представить в виде корреляционной матрицы – матрицы абсолютных частот (таблица 15):
| Таблица 15 – МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ | |
 |
В этой матрице в качестве классов (столбцов) приняты будущие состояния объекта управления, как целевые, так и нежелательные, а в качестве атрибутов (строк) – факторы, которые разделены на три основных группы, математически обрабатываемые единообразно: факторы, характеризующие текущее и прошлые состояния объекта управления; управляющие факторы системы управления; факторы, характеризующие прошлые, текущее и прогнозируемые состояния окружающей среды. Отметим, что форма таблицы 15 является универсальной формой представления и обобщения фактов – эмпирических данных
в единстве их дискретного и интегрального представления (причины – следствия, факторы – результирующие состояния, признаки – обобщенные образы классов, образное – логическое и т.п.).
Управляющие факторы объединяются в группы, внутри каждой из которых они альтернативны (несовместны), а между которыми - нет (совместны). В этом случае внутри каждой группы выбирают одно из доступных управляющих воздействий с максимальным влиянием. Варианты содержательной информационной модели без учета прошлых состояний объекта управления и с их учетом, аналогичны, соответственно, простым и составным цепям Маркова, автоматам без памяти и с памятью.
В качестве количественной меры влияния факторов, предложено использовать обобщенную формулу А.Харкевича (3.28), полученную на основе предложенной эмерджентной теории информации. При этом по формуле (3.28) непосредственно из матрицы абсолютных частот (таблица 15) рассчитывается матрица информативностей (таблица 16), которая и представляет собой основу содержательной информационной модели предметной области.
| Таблица 16 – МАТРИЦА ИНФОРМАТИВНОСТЕЙ | |
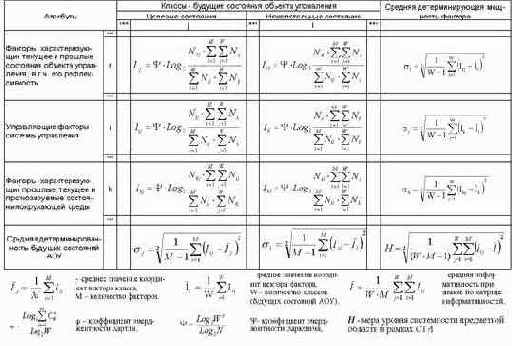 |
Весовые коэффициенты таблицы 3.28 непосредственно определяют, какое количество информации Iij система управления получает о наступлении события: "активный объект управления перейдет в j–е состояние", из сообщения: "на активный объект управления действует i–й фактор".
Принципиально важно, что эти весовые коэффициенты не определяются экспертами неформализуемым способом, а рассчитываются непосредственно
на основе эмпирических данных и удовлетворяют всем ранее сформулированным требованиям, т.е. являются сопоставимыми, содержательно интерпретируемыми, отражают понятия "достижение цели управления" и "мощность множества будущих состояний объекта управления" и т.д.
В данном исследовании обосновано, что предложенная информационная мера обеспечивает сопоставимость индивидуальных количеств информации, содержащейся в факторах о классах, а также сопоставимость интегральных критериев, рассчитанных для одного объекта и разных классов, для разных объектов и разных классов.
Когда количество информации Iij>0
– i–й фактор способствует переходу объекта управления в j–е
состояние, когда Iij<0 – препятствует этому переходу, когда же Iij=0 – никак не влияет на это. В векторе i–го
фактора (строка матрицы информативностей) отображается, какое количество информации о переходе объекта управления в каждое из будущих состояний содержится в том факте, что данный фактор действует. В векторе j–го состояния класса (столбец матрицы информативностей) отображается, какое количество информации о переходе объекта управления в соответствующее состояние содержится в каждом из факторов.
Таким образом, матрица информативностей (таблица 16) является обобщенной таблицей решений, в которой входы (факторы) и выходы (будущие состояния АОУ) связаны друг с другом не с помощью классических (Аристотелевских) импликаций, принимающих только значения: "Истина" и "Ложь", а различными значениями истинности, выраженными в битах
и принимающими значения от положительного теоретически-максимально-возможного ("Максимальная степень истинности"), до теоретически неограниченного отрицательного ("Степень ложности").
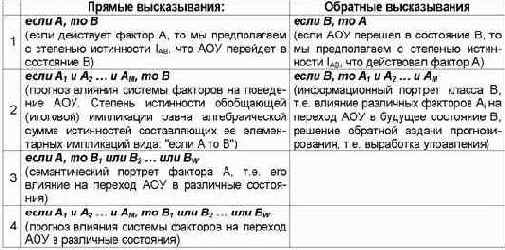
Фактически предложенная модель позволяет осуществить синтез обобщенных таблиц решений для различных предметных областей непосредственно на основе эмпирических исходных данных и продуцировать на их основе прямые и обратные правдоподобные (нечеткие) логические рассуждения по неклассическим схемам с различными расчетными значениями истинности, являющимся обобщением классических импликаций (таблица 17).
|
Таблица 17 – ПРЯМЫЕ И ОБРАТНЫЕ ПРАВДОПОДОБНЫЕ ЛОГИЧЕСКИЕ ВЫСКАЗЫВАНИЯ С РАСЧЕТНОЙ (В СООТВЕТСТВИИ С СТИ) СТЕПЕНЬЮ ИСТИННОСТИ ИМПЛИКАЦИЙ |
 |
Приведем пример более сложного высказывания, которое может быть рассчитано непосредственно на основе матрицы информативностей – обобщенной таблицы решений (таблица 16):
Если A, со степенью истинности a(A,B) детерминирует B, и если С, со степенью истинности a(C,D) детерминирует D, и A совпадает по смыслу с C со степенью истинности a(A,C), то это вносит вклад в совпадение B с D, равный степени истинности a(B,D).
При этом в прямых рассуждениях как предпосылки рассматриваются факторы, а как заключение – будущие состояния АОУ, а в обратных – наоборот: как предпосылки – будущие состояния АОУ, а как заключение – факторы. Степень истинности i-й предпосылки – это просто количество информации Iij, содержащейся в ней о наступлении j-го будущего состояния АОУ. Если предпосылок несколько, то степень истинности наступления j-го состояния АОУ равна суммарному количеству информации, содержащемуся в них об этом. Количество информации в i-м факторе о наступлении j-го состояния АОУ, рассчитывается в соответствии с выражением (3.28) СТИ.
Прямые правдоподобные логические рассуждения позволяют прогнозировать степень достоверности наступления события по действующим факторам, а обратные – по заданному состоянию восстановить степень необходимости и степень нежелательности каждого фактора для наступления этого состояния, т.е. принимать решение по выбору управляющих воздействий на АОУ, оптимальных для перевода его в заданное целевое состояние.
Необходимо отметить, что предложенная модель, основывающаяся на теории информации, обеспечивает автоматизированное формирования системы нечетких правил по содержимому входных данных, как и комбинация нечеткой логики Заде-Коско с нейронными сетями Кохонена. Принципиально важно, что качественное изменение модели путем добавления в нее новых классов не уменьшает достоверности распознавания уже сформированных классов.
Кроме того, при сравнении распознаваемого объекта с каждым классом учитываются не только признаки, имеющиеся у объекта, но и отсутствующие у него, поэтому предложенной моделью правильно идентифицируются объекты, признаки которых образуют множества, одно из которых является подмножеством другого (как и в Неокогнитроне К.Фукушимы) [197].
Данная модель позволяет прогнозировать поведение АОУ при воздействии на него не только одного, но и целой системы факторов:
 |
(3. 35) |
В теории принятия решений скалярная функция Ij
векторного аргумента называется интегральным критерием. Основная проблема состоит в выборе такого аналитического вида функции интегрального критерия, который обеспечил бы эффективное решение сформулированной выше задачи АСУ.
Учитывая, что частные критерии (3.28) имеют смысл количества информации, а информация по определению является аддитивной функцией, предлагается ввести интегральный критерий, как аддитивную функцию от частных критериев в виде:
 |
(3. 36) |
В выражении (3.54) круглыми скобками обозначено скалярное произведение. В координатной форме это выражение имеет вид:
 |
(3. 37) |
где:



В реализованной модели значения координат вектора состояния ПО принимались равными либо 1 (фактор действует), либо 0 (фактор не действует).
Таким образом, интегральный критерий
представляет собой суммарное количество информации, содержащееся в системе факторов различной природы (т.е. факторах, характеризующих объект управления, управляющее воздействие и окружающую среду) о переходе активного объекта управления в будущее (в т.ч. целевое или нежелательное) состояние.
В многокритериальной постановке задача прогнозирования состояния объекта управления, при оказании на него заданного многофакторного управляющего воздействия Ij, сводится к максимизации интегрального критерия:
 |
(3. 38) |
т.е. к выбору такого состояния объекта управления, для которого интегральный критерий максимален.
Задача принятия решения о выборе наиболее эффективного управляющего воздействия является обратной задачей по отношению к задаче максимизации интегрального критерия (идентификации и прогнозирования), т.е. вместо того, чтобы по набору факторов прогнозировать будущее состояние АОУ, наоборот, по заданному (целевому) состоянию АОУ определяется такой набор факторов, который с наибольшей эффективностью перевел бы объект управления в это состояние.
Предлагается еще одно обобщение этой фундаментальной леммы, основанное на косвенном учете корреляций между информативностями в векторе состояний при использовании средних по векторам. Соответственно, вместо простой суммы количеств информации предлагается использовать корреляцию между векторами состояния и объекта управления, которая количественно измеряет степень сходства этих векторов:
 |
(3. 39) |
где:




Выражение (3.39) получается непосредственно из (3.37) после замены координат перемножаемых векторов их стандартизированными значениями:

Результат прогнозирования поведения объекта управления, описанного данной системой факторов, представляет собой список его возможных будущих состояний, в котором они расположены в порядке убывания суммарного количества информации о переходе объекта управления в каждое из них.
Сравнения результатов идентификации и прогнозирования с опытными данными, с использованием выражений (3.37) и (3.39), показали, что при малых выборках они практически не отличаются, но при увеличении объема выборки до 400 и более (независимо от предметной области) выражение (3.39) дает погрешность идентификации (прогнозирования) на 5% – 7% меньше, чем (3.37).
Поэтому в предлагаемой модели фактически используется не метрическая мера сходства (3.39).
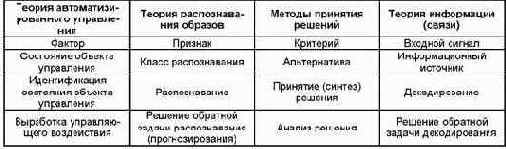
В связи с тем, что в дальнейшем изложении широко применяются понятия теории АСУ, теории информации (связи), теории распознавания образов и методов принятия решений, приведем таблицу соответствия наиболее часто используемых нами терминов из этих научных направлений, имеющих сходный смысл (таблица 18):
|
Таблица 18 – СООТВЕТСТВИЕ ТЕРМИНОВ РАЗЛИЧНЫХ НАУЧНЫХ НАПРАВЛЕНИЙ |
 |
Вывод системного обобщения формулы Харкевича (3.28) приведен в разделе 3.1 данной работы. Чрезвычайно важное для данного исследования выражение (3.28) заслуживает специального комментария. Прежде всего нельзя не обратить внимания на то, что оно по своей математической форме, т.е. формально, ничем не отличается от выражения для превышения сигнала над помехой для информационного канала [196]. Из этого, на первый взгляд, внешнего совпадения следует интересная интерпретация выражения (3.28). А именно: можно считать, что обнаружив некоторый i–й признак у объекта, предъявленного на распознавание, мы тем самым получаем сигнал, содержащий некоторое количество информации

о том, что этот объект принадлежит к j–му классу. По–видимому, это так и есть, однако чтобы оценить насколько много или мало этой информации нами получено, ее необходимо с чем–то сравнить, т.е. необходимо иметь точку отсчета или базу для сравнения. В качестве такой базы естественно принять среднее по всем признакам количество информации, которое мы получаем, обнаружив этот j–й класс:

Иначе говоря, если при предъявлении какого–либо объекта на распознавание у него обнаружен i–й признак, то для того, чтобы сделать из этого факта обоснованный вывод о принадлежности этого объекта к тому или иному классу, необходимо знать и учесть, насколько часто вообще (т.е. в среднем) обнаруживается этот признак при предъявлении объектов данного класса.
Фактически это среднее количество информации можно рассматривать как некоторый "информационный шум", который имеется в данном признаке и не несет никакой полезной информации о принадлежности объектов к тем или иным классам.
Полезной же информацией является степень отличия от этого шума. Таким образом классическому выражению Харкевича (3.12) для семантической целесообразности информации может быть придан более привычный для теории связи вид:

который интерпретируется как вычитание шума из полезного сигнала. Эта операция является совершенно стандартной в системах шумоподавления.
Если полезный сигнал выше уровня шума, то его обнаружение несет информацию в пользу принадлежности объекта к данному классу, если нет – то, наоборот, в пользу не принадлежности.
Возвращаясь к выражению (3.12), необходимо отметить, что сам А.А.Харкевич рассматривал




Необходимо отметить также, что каждый признак объекта управления как канала связи может быть охарактеризован динамическим диапазоном, равным разности максимально возможного (допустимого) уровня сигнала в канале и уровня помех в логарифмическом масштабе:

Максимальное количество информации, которое может содержаться в признаке, полностью определяется количеством классов распознавания W и равно количеству информации по Хартли: I=Log2W.
Динамический диапазон признака является количественной мерой его полезности (ценности) для распознавания, но все же предпочтительней для этой цели является среднее количество полезной для классификации информации в признаке, т.е. исправленное выборочное среднеквадратичное отклонение информативностей:
 |
(3. 40) |
Очевидна близость этой меры к длине вектора признака в семантическом пространстве атрибутов:
 |
(3. 41) |
В сущности выражение (3.40) просто представляет собой нормированный вариант (3.41).
