Системное обобщение формулы Хартли для количества информации

Классическая формула Хартли имеет вид:

(3. 1)

Будем искать ее системное обобщение в виде:

(3. 2)

где:

W – количество чистых (классических) состояний системы.

j – коэффициент эмерджентности Хартли (уровень системной организации объекта, имеющего W чистых состояний);

Учитывая, что возможны смешанные состояния, являющиеся нелинейной суперпозицией или одновременной реализацией чистых (классических) состояний "из W по m", всего возможно

состояний системы, являющихся сочетаниями классических состояний. Таким образом, примем за аксиому, что системное обобщение формулы Хартли имеет вид [64]:

(3. 3)

где: W – количество элементов в системе альтернативных будущих состояний АОУ (количество чистых состояний); m – сложность смешанных состояний АОУ; M – максимальная сложность смешанных состояний АОУ.

Выражение (1) дает количество информации в активной системе, в которой чистые и смешанные состояния равновероятны. Смешанные состояния активных систем, возникающие под действием системы нелинейно-взаимодействующих факторов, считаются такими же измеримыми, как и чистые альтернативные состояния, возникающие под действием детерминистских факторов. Так как

, то при M=1 выражение (3.3) приобретает вид (3.1), т.е. выполняется принцип соответствия, являющийся обязательным для более общей теории.

Рассмотрим подробнее смысл выражения (3.3), представив сумму в виде ряда слагаемых:

(3. 4)

Первое слагаемое в (3.4) дает количество информации по классической формуле Хартли, а остальные слагаемые – дополнительное количество информации, получаемое за счет системного эффекта, т.е. за счет наличия у системы иерархической структуры или смешанных состояний. По сути дела эта дополнительная информация является информацией об иерархической структуре системы, как состоящей из ряда подсистем  различных уровней сложности.

Например, пусть система состоит из W пронумерованных элементов 1-го уровня иерархии. Тогда на 2-м уровне иерархии элементы соединены в подсистемы из 2 элементов 1-го уровня, на 3-м – из 3, и т.д.
Если выборка любого элемента равновероятна, то из факта выбора n-го элемента по классической формуле Хартли мы получаем количество информации согласно (3.1). Если же при этом известно, что  данный элемент входит в определенную подсистему 2-го уровня, то это дает дополнительное количество информации, за счет учета второго слагаемого, поэтому общее количество получаемой при этом информации будет определяться выражением (3.4) уже с двумя слагаемыми (M=2). Если элемент одновременно входит в M подсистем разных уровней, то количество информации, получаемое о системе и ее подсистемах при выборке этого элемента определяется выражением (3.4). Так, если мы вытаскиваем кирпич из неструктурированной кучи, состоящей из 32 кирпичей, то получаем 5 бит информации, если же из этих кирпичей сложен дом, то при аналогичном действии мы получаем дополнительное количество информации о том, из каких части дома (подсистем различного уровня иерархии) вытащен этот кирпич. Действия каменщика, укладывающего кирпич на место, предусмотренное проектом, значительно выше по целесообразности, чем у грузчика, складывающего кирпичи в кучу. Учитывая, что при M=W:

(3. 5)

в этом случае получаем:

(3. 6)

Выражение (3.5) дает оценку максимального количества информации, которое может содержаться в элементе системы с учетом его вхождения в различные подсистемы ее иерархической структуры.

Однако реально в любой системе осуществляются не все формально возможные сочетания элементов 1-го уровня иерархии, т.к. существуют различные правила запрета, различные для разных систем. Это означает, что возможно множество различных систем, состоящих из одинакового количества тождественных элементов, и отличающихся своей структурой, т.е. строением подсистем различных иерархических уровней. Эти различия систем как раз и возникают благодаря различию действующих для них этих правил запрета. По этой причине систему правил запрета предлагается назвать информационным проектом системы. Различные системы, состоящие из равного количества одинаковых элементов (например, дома, состоящие из 20000 кирпичей), отличаются друг от друга именно по причине различия своих информационных проектов.



Из выражения (3.5) очевидно, что I быстро стремится к W:

(3. 7)

В действительности уже при W>4 погрешность выражения (3.5) не превышает 1% (таблица 9):

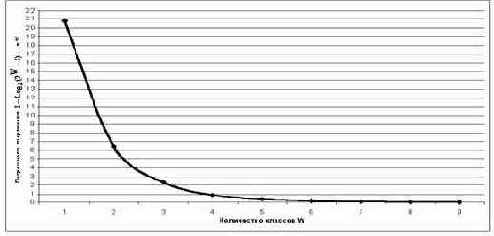
Таблица 9 – ЗАВИСИМОСТЬ ПОГРЕШНОСТИ ВЫРАЖЕНИЯ (3.5) ОТ КОЛИЧЕСТВА КЛАССОВ  W

График зависимости погрешности выражения (3.5) от количества классов W приведен на рисунке 24.

Рисунок 24. Зависимость погрешности приближенного выражения системного обобщения формулы Хартли от количества классов W

Приравняв правые части выражений (3.2) и (3.3):

(3. 8)

получим выражение для коэффициента эмерджентности Хартли (терм. авт.):

(3. 9)

Непосредственно из вида выражения для коэффициента эмерджентности Хартли (3.9) ясно, что он представляет собой относительное превышение количества информации о системе при учете системных эффектов (смешанных состояний, иерархической структуры ее подсистем и т.п.) над количеством информации без учета системности, т.е. этот коэффициент отражает уровень системности объекта.

С учетом выражения (3.9) выражение (3.2) примет вид:

(3. 10)

или при M=W и больших W, учитывая (3.4 – 3.6):

(3. 11)

Выражение (3.10) и представляет собой искомое системное обобщение классической формулы Хартли, а выражение (3.11) – его достаточно хорошее приближение при большом количестве элементов или состояний системы (W).

Коэффициент эмерджентности Хартли представляет собой относительное превышение количества информации о системе при учете системных эффектов (смешанных состояний, иерархической структуры ее подсистем и т.п.) над количеством информации без учета системности, т.е. этот коэффициент является аналитическим выражением для уровня системности объекта. Таким образом, коэффициент эмерджентности Хартли отражает уровень системности объекта и изменяется от 1 (системность минимальна, т.е. отсутствует) до W/Log2W (системность максимальна). Очевидно, для каждого количества элементов системы существует свой максимальный уровень системности, который никогда реально не достигается из-за действия правил запрета



на реализацию в системе ряда подсистем различных уровней иерархии.

Например: из 32 букв русского алфавита может быть образовано не  осмысленных 6-буквенных слов, а значительно меньше. Если мы услышим одно из этих в принципе возможных слов, то получим не 5´6=30 информации, содержащейся непосредственно в буквах (в одной букве содержится Log232=5 бит), а 30+19,79=49,79 бит, т.е. в 1.66 раз больше. Это и есть уровень системности иерархического уровня 6-буквенных слов русского языка. Уровень системности русского языка, как системы, состоящей из слов длиной от одной до 6 букв, согласно выражения (3.9) с учетом (3.5), равен примерно 6,4. Но при этом еще не была учтена информация, содержащаяся в последовательности слов, в последовательности предложений и т.д.

Итак, в предложении сдержится значительно больше информации, чем в буквах, с помощью которых оно написано, т.к. кроме букв информацию содержат слова, сочетания слов, последовательность предложений и т.д.. Буквы образуют 1-й иерархический уровень языка, слова – 2-й, предложения – 3-й, абзацы – 4-й, параграфы – 5-й, главы – 6-й, произведения – 7-й. Теория Шеннона концентрирует основное внимание на рассмотрении 1-го уровня, т.е. рассматривает тексты, прежде всего, как последовательность символов. Но именно иерархическая организация, не учитываемая в теории Шеннона и отраженная в системной теории информации,  обеспечивает языку его удивительную мощь, как средства отражения и моделирования реальности.

Аналогично и в генах, этих своеобразных "символах генома", содержится значительно больше информации о фенотипе, чем предполагается в классической генетике Менделя, т.к. гены образуют ансамбли различных уровней иерархии в зависимости от влияния среды и технологий управления (явление адаптивности системы "генотип-среда", Драгавцев В.А., 1993). Если ген уподобить букве алфавита, а смысл фразы – фенотипическому признаку, то можно сказать, что возможно очень большое количество фраз с одним и тем же смысловым содержанием (тогда как в классической генетике считалось, что признак соответствует гену, хотя есть и такие).


После расшифровки генома человека мы настолько же приблизились к его пониманию, как изучивший русскую или немецкую азбуку англичанин, не знающий этих языков, приблизился к чтению в оригинале и пониманию содержания "Войны и Мира" Льва Толстого или "Феноменологии Духа" Георга В.Ф.Гегеля.

На уровне слов верхняя оценка уровня системности русского языка с учетом (3.5) составляет огромную величину: 2616,48 (предполагается, что в русском языке 40000 слов и предложения могут иметь любую длину). Необходимо отметить, что правила запрета на порядок слов в русском языке значительно слабее, чем, например в английском, поэтому в русском языке возможно гораздо больше грамматически правильных и несущих различную информацию предложений из одних и тех же слов, чем в английском. Это значит, что уровень системности русского языка на уровне предложений, по-видимому, значительно превосходит уровень системности английского языка. При длине предложения до 2-х слов системность русского языка на уровне предложений согласно (3.9) составляет: 52330916.

Анализ выражения (3.9) показывает, что при М=1 оно преобразуется в (3.1), т.е. выполняется принцип соответствия. При М>1 количество информации в соответствии с системной теорией информации (СТИ) (3.9) будет превосходить количество информации, рассчитанное по классической теории информации (КТИ) (3.1). Непосредственно из выражения (3.2) получаем:

(3. 12)

Первое слагаемое в выражении (3.12) отражает количество информации, согласно КТИ, а второе – СТИ, т.е. доля системной информации.

Представляет несомненный интерес исследование закономерностей изменения доли системной информации в поведении элемента системы в зависимости от количества классов W и сложности смешанных состоянийM.

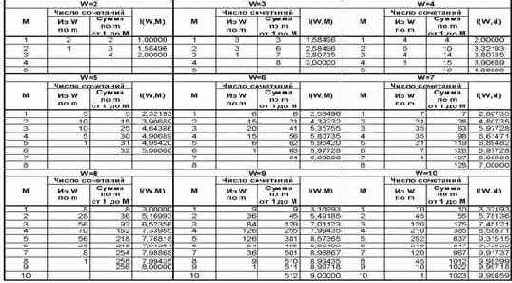
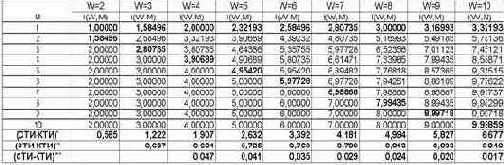
В таблице 10 приведены результаты численных расчетов в соответствии с выражением (3.9). Сводные данные из таблицы 10 приведены в таблице 11, а в графическом виде они представлены на рисунке 25.

Таблица 10 – ЗАВИСИМОСТЬ I(W,M) ОТ КОЛИЧЕСТВА КЛАССОВ W И СЛОЖНОСТИ СМЕШАННЫХ СОСТОЯНИЙ М

Таблица 11 – ЗАВИСИМОСТЬ КОЛИЧЕСТВА ИНФОРМАЦИИ I(W,M) ОТ СЛОЖНОСТИ СМЕШАННЫХ СОСТОЯНИЙ M ДЛЯ РАЗЛИЧНОГО КОЛИЧЕСТВА КЛАССОВ W

<

Рисунок 25. Зависимость количества информации I(W,M) от сложности смешанных состояний M для разного количества классов W

Рост количества информации в СТИ по сравнению с КТИ обусловлен системным эффектом (эмерджентностью), который связан с учетом смешанных состояний, возникающих путем одновременной реализации (суперпозиции) нескольких чистых (классических) состояний под действием системы нелинейно-взаимодействующих недетерминистских факторов. Выражение (3.9) дает максимальную возможную оценку количества информации, т.к. могут существовать различные правила запрета на реализацию тех или иных смешанных состояний.

Фактически это означает, что в СТИ множество возможных состояний объекта рассматривается не как совокупность несвязанных друг с другом состояний, как в КТИ, а как система, уровень системности которой как раз и определяется коэффициентом эмерджентности Хартли j (3.9), являющегося монотонно возрастающей функцией сложности смешанных состояний M. Следовательно, дополнительная информация, которую мы получаем из поведения объекта в СТИ, по сути дела является информацией о системе всех возможных состояний объекта, элементом которой является объект в некотором данном состоянии.


Содержание раздела

---

---