Системное обобщение классической формулы Харкевича, как количественная мера знаний

Это обобщение представляет большой интерес, в связи с тем, что А.Харкевич впервые ввел в теорию информации понятие цели.

Он считал, что количество информации, сообщенное объекту, можно измерять по изменению вероятности достижения цели этим объектом за счет использования им этой информации.

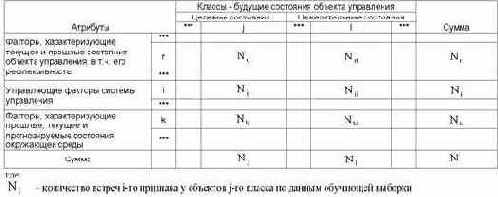
Рассмотрим таблицу 12, в которой столбцы соответствуют будущим состояниям АОУ (целевым и нежелательным), а строки факторам, характеризующим объект управления, управляющую систему и окружающую среду.

Таблица 12 – МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ

Классическая формула А.Харкевича имеет вид:

(3. 19)

где:

– W – количество классов (мощность множества будущих состояний объекта управления)

– M – максимальный уровень сложности смешанных состояний объекта управления;

– индекс i обозначает фактор: 1£ i £ M;

– индекс j обозначает класс: 1£ j £ W;

– Pij – вероятность достижения объектом управления j-й цели при условии сообщения ему i-й информации;

– Pj – вероятность самопроизвольного достижения объектом управления j-й цели.

Ниже глобальные параметры модели W и M в выражениях для I опускаются, т.к. они являются константами для конкретной математической модели СК-анализа.

Однако: А.Харкевич в своем выражении для количества информации не ввел зависимости количества информации, от мощности пространства будущих состояний объекта управления, в т.ч. от количества его целевых состояний. Вместе с тем, один из возможных вариантов учета количества будущих состояний объекта управления обеспечивается классической и системной формулами Хартли (3.1) и (3.9); выражение (3.19) при подстановке в него реальных численных значений вероятностей Pij и Pj не дает количества информации в битах; для выражения (3.19) не выполняется принцип соответствия, считающийся обязательным для обобщающих теорий. Возможно, в этом состоит одна из причин слабого взаимодействия между классической теорией информации Шеннона и семантической теорией информации.

Чтобы снять эти вопросы, приближенно выразим вероятности Pij, Pi и Pj через частоты:

(3. 20)

В (3.20) использованы обозначения:

Nij – суммарное количество наблюдений факта: "действовал i-й фактор и объект перешел в j-е состояние";

Nj – суммарное количество встреч различных факторов у объектов, перешедших в j-е состояние;

Ni – суммарное количество встреч i-го фактора у всех объектов;

N – суммарное количество встреч различных факторов у всех объектов.

Подставим в выражение (3.19) значения для Pij

и Pj из (3.20):

(3. 21)

Введем коэффициент эмерджентности Y в модифицированную формулу А.Харкевича:

(3. 22)

где: Y – коэффициент эмерджентности Харкевича (как будет показано выше, он определяет степень детерминированности объекта с уровнем системной организации j, имеющего W чистых состояний, на переходы в которые оказывают влияние M факторов, о чем в модели накоплено N фактов).

Известно, что классическая формула Шеннона для количества информации для неравновероятных событий преобразуется в формулу Хартли при условии, что события равновероятны, т.е. удовлетворяет фундаментальному принципу соответствия[64].

Естественно потребовать, чтобы и обобщенная формула Харкевича также удовлетворяла аналогичному принципу соответствия, т.е. преобразовывалась в формулу Хартли в предельном случае, когда каждому классу (состоянию объекта) соответствует один признак (фактор), и каждому признаку – один класс, и эти классы (а, значит и признаки), равновероятны. Иначе говоря факторов столько же, сколько и будущих состояний объекта управления, все факторы детерминистские, а состояния объекта управления – альтернативные, т.е. каждый фактор однозначно определяет переход объекта управления в определенное состояние.

В этом предельном случае отпадает необходимость двухвекторного описания объектов, при котором 1-й вектор (классификационный) содержит интегральное описание объекта, как принадлежащего к определенным классам, а 2-й вектор (описательный) – дискретное его описание, как имеющего определенные атрибуты. Соответственно, двухвекторная модель, предложенная в данной работе, преобразуется в "вырожденный" частный случай – стандартную статистическую модель.

В этом случае количество информации, содержащейся в признаке о принадлежности объекта к классу является максимальным

и равным количеству информации, вычисляемому по системной формуле Хартли (3.9).

Таким образом при взаимно-однозначном соответствии классов и признаков:

(3. 23)

формула А.Харкевича (3.13) приобретает вид:

(3. 24)

откуда:

(3. 25)

или, учитывая выражение для коэффициента эмерджентности Хартли (3.8):

(3. 26)

Смысл коэффициента эмерджентности Харкевича (3.25) проясняется, если учесть, что при количестве состояний системы W равном количеству фактов N о действии на эту систему различных факторов он равен 1. В этом случае факторы однозначно определяют состояния объекта управления, т.е. являются детерминистскими. Если же количество фактов N о действии на эту систему различных факторов превосходит количество ее состояний W, что является гораздо более типичным случаем, то этот коэффициент меньше 1. По-видимому, это означает, что в этом случае факторы как правило не однозначно (и не так жестко как детерминистские) определяют поведение объекта управления, т.е. являются статистическими.

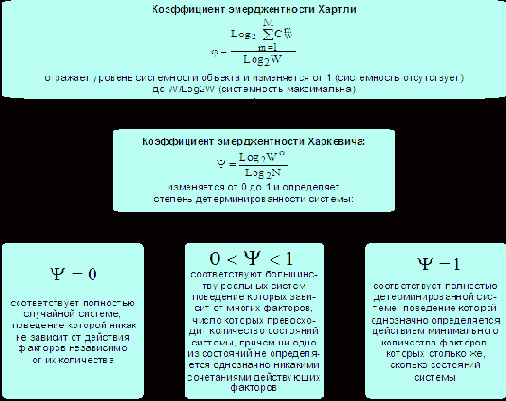
Таким образом, коэффициент эмерджентности Харкевича Y изменяется от 0 до 1 и определяет степень детерминированности системы:

– Y=1 соответствует полностью детерминированной системе, поведение которой однозначно определяется действием минимального количества факторов, которых столько же, сколько состояний системы;

– Y=0 соответствует полностью случайной системе, поведение которой никак не зависит действия факторов независимо от их количества;

– 0<Y<1 соответствуют большинству реальных систем поведение которых зависит от многих факторов, число которых превосходит количество состояний системы, причем ни одно из состояний не определяется однозначно никакими сочетаниями действующих факторов (рисунок 29):

Рисунок 29. Интерпретация коэффициентов эмерджентности СТИ

Из выражения (3.25) видно, что в частном случае, когда реализуются только чистые состояния объекта управления, т.е.

M=1, коэффициент эмерджентности А.Харкевича приобретает вид:

(3. 27)

Подставив коэффициент эмерджентности А.Харкевича (3.25) в выражение (3.22), получим:

или окончательно:

(3. 28)

Из вида выражения (3.25) для Y очевидно, что увеличение уровня системности влияет на семантическую информационную модель (3.28) аналогично повышению уровня детерминированности системы: понижение уровня системности, также как и степени детерминированности системы приводит к ослаблению влияния факторов на поведение системы, т.е. к понижению управляемости системы за счет своего рода "инфляции факторов".

Например: управлять толпой из 1000 человек значительно сложнее, чем воздушно-десантным полком той же численности. Процесс превращения 1000 новобранцев в воздушно-десантный полк это и есть процесс повышения уровня системности и степени детерминированности системы. Этот процесс включает процесс иерархического структурирования (на отделения, взвода, роты, батальоны), а также процесс повышения степени детерминированности команд, путем повышения "степени беспрекословности" их исполнения. Оркестр, настраивающий инструменты, также весьма существенно отличается от оркестра, исполняющего произведение под управлением дирижера.

Необходимо отметить, что при повторном использовании той же самой обучающей выборки степень детерминированности модели уменьшается. Очевидно, с формальной математической точки зрения этого явления можно избежать, если перед расчетом информативностей признаков делить абсолютные частоты на количество объектов обучающей выборки.

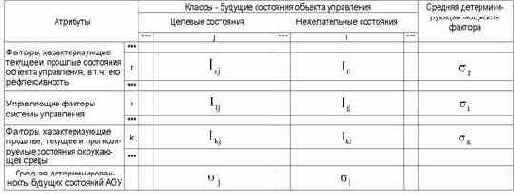
С использованием выражения (3.28) непосредственно из матрицы абсолютных частот (таблица 12) рассчитывается матрица информативностей (таблица 13), содержащая связи между факторами и будущими состояниями АОУ и имеющая много различных интерпретаций и играющая основополагающую роль в данном исследовании.

Таблица 13 – МАТРИЦА ИНФОРМАТИВНОСТЕЙ

Из рассмотрения основополагающего выражения (3.28) видно, что:

1. При выполнении условий взаимно-однозначного соответствия классов и признаков (3.23) первое слагаемое в выражении (3.28) обращается в ноль и при всех реальных значениях входящих в него переменных оно отрицательно.

2. Выражение (3.28) является нелинейной суперпозицией двух выражений: системного общения формулы Хартли (второе слагаемое), и первого слагаемого, которое имеет вид формулы Шеннона для плотности информации и отличается от него тем, что выражение под логарифмом находится в степени, которая совпадает с коэффициентом эмерджентности Харкевича, а также способом взаимосвязи входящих в него абсолютных частот с вероятностями.

Это дает основание предположить, что первое слагаемое в выражении (3.28) является одной из форм системного обобщения выражения Шеннона для плотности информации:

(3. 29)

Поэтому вполне оправданным будет назвать степень в (3.29) коэффициентом эмерджентности Шеннона-Харкевича.

Содержание раздела