Разветвленные алгоритмы
Разветвленные алгоритмы в своем составе содержат блок условия и различные конструкции ветвления. Ветвление
- это структура, обеспечивающая выбор между альтернативами.
 |
 |
 |
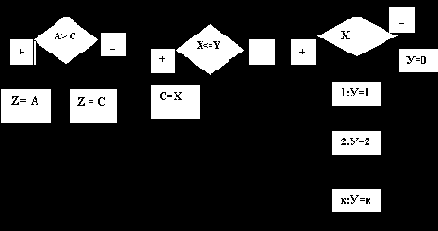
а) ветвление б)неполное ветвление в) многоальтернативный выбор
Рис. 4. Структуры ветвления
Каждая управляющая структура ветвления имеет один вход и один выход. Ветвления содержат блок условия, в котором записывают логические условия, такие как А >С , X<= Y. В зависимости от значений переменных А,С в управляющей структуре ветвления на рис. 4 а) условие А >С принимает значение "истина" или "ложь" и процесс вычислений включает блок действия Z=A или Z=C. Аналогично происходит и в управляющей структуре неполного ветвления (рис. 4 б)). Только в этом случае , если условие X<= Y истинно, то выполняется действие С=Х, в противном случае никаких действий не выполняется.
В управляющей структуре многоальтернативный выбор в блоке условия записывается переменная, в данном случае Х, которая может принимать различные значения (рис. 4в)). Если значение пременной Х совпадет с одним из значений в блоке действия, то выполняется действия , записанные в этом блоке. Например, если Х=1, то выполнится действие У=1. Если значение Х не совпало ни с одним из значений, указанных в блоках справа, то выполняется действие в блоке слева, которого также как и в неполном ветвлении может и не быть.
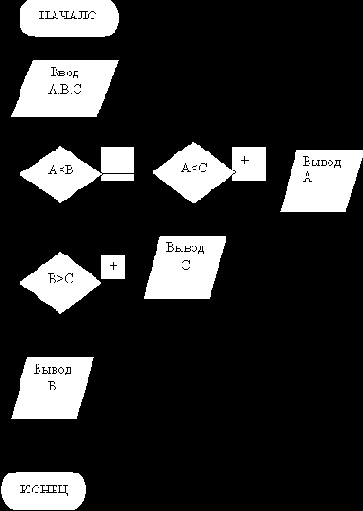
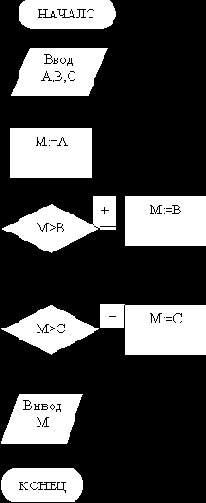
Пример 2.Составить алгоритм нахождения минимального значения из 3-х чисел. Решение. Для определения минимального значения будем использовать проверку пары значений. Визуальные разветвленные алгоритмы приведены на рис.5,6,7. Эти алгоритмы использует для обозначения чисел переменные значения А,В,С и вложенные структуры ветвления.
 |
 |
Рис. 5. Поиск минимального значения из трех чисел A,B,C при помощи двойного сравнения.
 |
 |
 |
Метод последовательного сравнения .
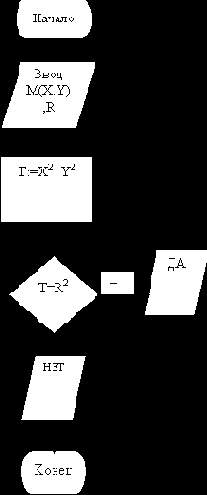
Пример 3. Составить алгоритм определения находится ли точка М с координатами Х,У на окружности радиуса R.
Решение.
Визуальный алгоритм приведен на рис. 8.Для решения в нем используется математическая модель в виде формулы окружности R2 = X2+Y2.
 |
 |
||
числа из трёх А,В,С. Метод ся ли точка М с координа-
сравнения с промежуточной ми Х,У на окружности
переменной М. радиуса R.
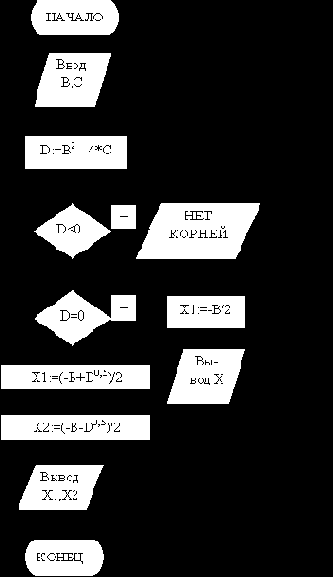
Пример 4. Составить алгоритм определения корней уравнения (X2+B*X+C=0).
Решение.
При составления этого алгоритма надо рассмотреть случаи, когда уравнение не имеет корней и когда имеется только один корень.Обозначим корни уравнения через переменные Х1,Х2. D - промежуточная переменная для вычисления дискриминанта. Алгоритм вычисления корней уравнения заданного вида приведен на рис. 9.
 |
