Решение задач динамики

Предисловие.

Содержание данной книги можно условно разделить на две части. Первая часть содержит инструкцию по гармоническому анализу, динамическому анализу переходных процессов, спектральному анализу. Здесь подробно рассмотрены особенности этих программ, возможные опции их применения, приведены некоторые примеры. Например, в главах, посвященных гармоническому анализу и анализу переходных процессов, рассматривается три возможных метода: полный, усеченный (редуцированный) с применением главных степеней свободы, и метод суперпозиции мод. Обсуждаются достоинства и недостатки каждого из этих способов.

Вторая часть посвящена некоторым теоретическим иллюстрациям вопросов, рассматриваемых в первой части. Например, рассмотрены теоретические основы метода суперпозиции мод (в отечественной литературе он называется методом разложения по собственным формам). Кратко рассмотрены вопросы случайных колебаний. Кратко рассмотрены вопросы однофакторного и многофакторного анализа, а так же вопросы взаимной корреляции спектральных плотностей. Безусловно, этот обзор ни в коем случае не претендует на полноту и служит лишь иллюстрацией первой части.

1. ГАРМОНИЧЕСКИЙ АНАЛИЗ

1.1. Введение

Циклическая нагрузка будет приводить к гармонической реакции механических систем. Гармонический анализ используется для нахождения установившейся реакции линейных систем, нагруженных синусоидальными силами. Расчет выполняется нахождением реакции системы на нескольких частотах и строится график амплитудно-частотной характеристики. Максимум реакции, найденный по графику будет соответствовать и максимуму напряжения в конструкции. Гармонический анализ предназначен для отыскания максимального значения уровней установившейся вибрации. Переходные процессы не оцениваются в этом виде анализа.

Гармонический анализ является линейным анализом. Некоторые нелинейности, такие как пластичность, контактные явления, или зазоры будут игнорироваться, даже если они определены в системе. Гармонический анализ может применяться в преднапряженных конструкциях, таких как скрипичная струна (при предположении, что напряжение от гармонической нагрузки существенно меньше, чем от предварительного напряжения).

Существуют три метода анализа: полный, усеченный и метод суперпозиции мод. (четвертый, сравнительно «дорогой» - метод анализа переходных процессов при гармонической нагрузке, представленной как функция времени). Программа ANSYS/Linear Plus допускает использование только метода суперпозиции мод. Перед изучением способов использования этих методов, рассмотрим достоинства и недостатки каждого метода.
1.2 Полный метод
Полный метод наиболее простой из этих трех методов. Он использует полную систему матриц для расчета амплитуд гармонической вибрации. Матрицы могут быть симметричными и не симметричными. Преимуществами полного метода являются:

Его легче использовать, потому что вы не должны беспокоиться о выборе главных степеней свободы, или собственных форм;
Он использует полные матрицы, так что аппроксимация матрицы масс не нужна;
Он позволяет использовать не симметричные матрицы, которые являются типичными для некоторых приложений, в частности для задач акустики;
Он рассчитывает перемещения и напряжения;

Он поддерживает все виды нагрузок: силы в узлах, заданные (не нулевые) перемещения, нагрузки на элементы (давления и температуры).
Он позволяет эффективно использовать твердотельные нагрузки.

Недостатком метода является то, что он не позволяет учитывать предварительное нагружение. Другим недостатком метода является, что он сравнительно «дорогой» по сравнению с двумя другими методами. 1.3 Усеченный метод. Усеченный метод позволяет вам сокращать размер задачи путем использования главных степеней свободы системы и сокращенных матриц. После расчета перемещений по главным степеням свободы решение может быть расширено для первоначального, полного набора степеней свободы. Преимущества этого метода:

Он работает быстрее и является менее «дорогим» по сравнению с полным методом;
Он учитывает эффект предварительного нагружения;

Недостатки этого метода:

В первом шаге вычисляются только перемещения по главным степеням свободы. Во втором шаге определяются полные перемещения и напряжения;
Нагрузки элементов (давление, температура) не учитываются;
Все нагрузки могут прикладываться только к главным степеням свободы, выбранных пользователем. (Это ограничивает применение твердотельных нагрузок);

1.4 Метод суперпозиции мод. Метод суперпозиции мод основан на суммировании факторов собственных мод из модального анализа.

Его преимущества:

Он работает быстрее, чем полный и усеченный методы для большинства задач;
Нагрузки на элементы, приложенные в (предшествующем) модальном анализе могут быть приложены в гармоническом анализе с помощью команды LVSCALE;
Он позволяет «сгущать» решение в диапазонах собственных частот конструкции. Это позволяет получить более точные кривые реакции;
Эффекты предварительного нагружения могут быть учтены;
Этот метод учитывает модальное демпфирование (как функцию частоты).

Недостатки метода:

Не нулевые заданные перемещения не применяются;
Когда используется программа POWER DYNAMICS для нахождения собственных частот (модальный анализ) начальные условия не могут иметь предварительно приложенных нагрузок.

Все три метода имеют общие ограничения:

Все нагрузки должны иметь синусоидальный закон изменения во времени;
Все нагрузки должны иметь одну и ту же частоту;
Нелинейности не учитываются;
Переходные режимы не рассчитываются.

Вы можете обойти некоторые из этих ограничений применением нестационарного динамического анализа с гармоническими нагрузками, представленными как функция времени.
2.     Решение задачи гармонического анализа.
Вначале мы приведем подробное описание гармонического анализа с использованием полного метода, а затем приведем различия для усеченного метода и метода суперпозиции мод.
Процедура решения задачи состоит из трех основных этапов:
1.     Построение модели.
2.     Приложение нагрузок и получение решения.
3.     Оценка результатов.
Построение модели. На этом этапе вы определяете имя задачи, заголовок задачи затем, используя препроцессор, определяете тип элементов, реальные константы, свойства материалов и геометрию модели.
Примечание 1) При гармоническом анализе учитывается только линейное поведение модели. Нелинейные элементы будут интерпретироваться как линейные. Например, если вы включили в модель контактные элементы, их жесткость рассчитывается на начальном этапе, и не изменяется в дальнейшем.

Примечание 2) Должны быть обязательно определены модуль упругости EX (или жесткость в любой другой форме) и плотность (DENS) (или массы). Свойства материалов должны быть линейные изотропные или ортотропные, температурно-зависимые или постоянные. Нелинейные свойства материалов игнорируются.
2.1. Приложение нагрузок и получение решения.
На этом этапе вы определяете тип анализа и его опции, прикладываете нагрузки, определяете опции шагов нагрузки и инициируете решение.
Максимальная реакция системы будет находиться на частотах, совпадающих с ее собственными частотами. Перед решением задачи гармонического анализа полезно определить собственные частоты из модального анализа.
1.     Войдите в режим решения с помощью команды /SOLU или в интерфейсе: Main Menu > Solution
2.     Определите тип анализа и его опции (табл. 2.1)
Тип анализа и его опции.
Таблица 2.1

Опции	Команда	Действия в интерфейсе
New Analysis	ANTYPE	Main Menu > Solution> Analysis Type- New Analys
Analysis Type: Harmonic Response	ANTYPE	Main Menu > Solution> Analysis Type- New Analis>Harmonic Response
Метод решения	HR OPT	Main Menu > Solution> Analysis Option
Формат вывода	HR OUT	Main Menu > Solution> Analysis Option
Вид матрицы масс	LUMPM	Main Menu > Solution> Analysis Option
Программа решения	EQSLV	Main Menu > Solution> Analysis Option

.
Каждая из этих опций подробно обсуждается далее.
Опция New Analysis используется, если вам необходимо приложить новую гармоническую силу.
Опция Harmonic Response определяет тип анализа- гармонический анализ.
Опция метод решения позволяет вам выбрать один из следующих методов:

Полный метод (Fool method);
Усеченный метод (Reduced method);
Метод суперпозиции мод (Mode superposition method).

Опция формат вывода (Solution Listing Format) позволяет определить как гармонические перемещения будут выводиться на печать (Jobname.OUT).

Вы можете выбрать, чтобы выводилась действительная и мнимая часть, или амплитуда и фазовый угол.
Опция вид матрицы масс (LUMPM).
Эта опция используется по умолчанию или соответствует аппроксимации матрицы масс сосредоточенными массами (в этом случае матрица масс имеет диагональный вид). Мы рекомендуем значение этой опции принимать по умолчанию для большинства приложений. Для некоторых задач, использующих “тонкие” системы, такие, как тонкие балки или очень тонкие оболочки, аппроксимация матрицы масс с помощью сосредоточенных масс часто приводит к лучшим результатам. Аппроксимация матрицы масс при помощи сосредоточенных масс требует меньшего времени решения и памяти.
После заполнения всех полей диалогового «ящика» опций гармонического анализа нажмите на кнопку «ОК» и появится второй диалоговый «ящик», где вы выберете метод решения.
Опция «Метод решения» [EQSLV]. Вы можете выбрать фронтальный метод (по умолчанию), метод соединенных градиентов Якоби (JCG), метод неполных соединенных градиентов Холецкого (ICCG). Фронтальный метод рекомендуется для большинства задач механики.
3. Приложение нагрузок к модели.
Гармонический анализ по определению предполагает, что приложенные нагрузки изменяются по синусоидальному закону по времени. Для полного описания гармонических нагрузок используется три параметра: амплитуды, фазовые углы, частотный диапазон (рис 2.1).

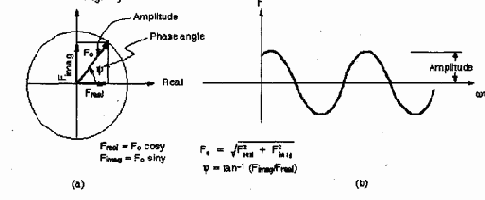Рис. 2.1.
Амплитуда – это максимальное значение нагрузки, которые выбираются с использованием команд, приведенных в таблице 2.2.
Фазовый угол – это измеренное время, на которое нагрузка запаздывает или опережает относительно заданного момента времени. На комплексной диаграмме (см. рис 2.1) этот угол измеряется относительно действительной оси. Фазовый угол требуется только в том случае, если имеется несколько нагрузок, отличающихся по фазам. Например, вращение неуравновешенной антенны, показанной на рис. 2.2 будет приводить к вертикальным нагрузкам в четырех опорных точках с различными фазовыми углами.

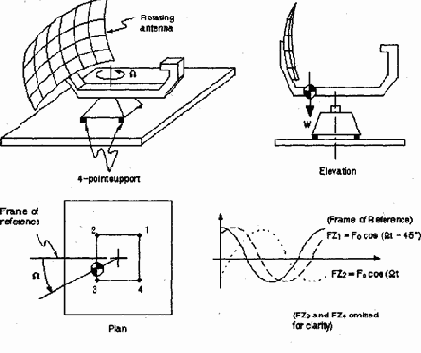Рис.2.2 Фазовый угол не может быть введен непосредственно. Для этого необходимо определить действительную и мнимую компоненту, используя значение VALUE1 и VALUE2 в соответствующей команде задания нагрузки. На рис. 2.1 показано, как определять действительную и мнимую компоненты.
Частотный диапазон представляет собой диапазон частот гармонической нагрузки. Он определяется позже, в опции шагов нагрузки с помощью команды HARFRQ.
Замечание 1. Гармонический анализ не может рассчитывать реакцию от одновременного действия нескольких сил, имеющих различные частоты, например от двух машин с различными угловыми скоростями, действующими одновременно. Хотя, можно использовать POST1 для учета совместного действия этих сил.
В таблице 2.2 приведены нагрузки, применимые для статического анализа. Исключение составляют инерционные нагрузки, которые вы можете приложить к твердотельной модели (точки, линии, поверхности), или к конечно-элементной модели (узлы и элементы).
Нагрузки, применяемые в гармоническом анализе. Таблица 2.2.

Тип нагрузки	Категория	Семейство команд	Интерфейс
Перемещения UX, UY, UZ, ROTX, ROTY, ROTZ	Закрепление	D	Main Menu > Solution> Load-Apply>Structural-Displasement
Сила, момент FX, FY, FZ, MX, MY, MZ	Силы	F	Main Menu > Solution> Load-Apply>Structural-Force/Moment
Давление (PRES)	Поверхностные нагрузки	SF	Main Menu > Solution> Load-Apply>Structural-Pressure
Температура (TEMP) Обтекание (FLUE)	Объемные нагрузки	BF	Main Menu > Solution> Load-Apply>Structural-Temperature
Гравитация, вращение и т.д.	Инерционные нагрузки	-	Main Menu > Solution> Load-Apply>Structural-Other

В процессе решения задачи нагрузки могут быть приложены, перемещены, распечатаны, или с ними могут быть произведены математические операции. В таблице 2.3 приведены команды операций с нагрузками для гармонического анализа.

Команды операций с нагрузками Таблица 2.3

Тип нагрузки	Твердотельная модель или КЭМ	Объекты	Приложение	Уничтожение	Печать	Операции	Опции
1	2	3	4	5	6	7	8
Перемещение	Твердотельная	Точки	DK	DKDELE	DKLIST	DTRAN	-
Перемещение	Твердотельная	Линии	DL	DLDELE	DLLIST	DTRAN	-
Перемещение	Твердотельная	Поверхности	DA	DADELE	DALIST	DTRAN	-

Продолжение табл. 2.3

1	2	3	4	5	6	7	8
Перемещение	КЭМ	Узлы	D	DDELE	DLIST	DSCALE	DSYM DCUM
Сила	Твердотельная	Точки	FK	FKDELE	FKLIST	FTRAN	-
Сила	КЭМ	Узлы	F	FDELE	FLIST	FSCALE	FCUM
Давление	Твердотельная	Линии	SFL	SFLDELE	LSFLLIST	SFTRAN	SFGRAD
Давление	Твердотельная	Поверхности	SFA	SFADELE	SFALIST	SFTRAN	SFGRAD
Давление	КЭМ	Узлы	SF	SFDELE	SFLIST	SFSCALE	SFGRAD SFCUM
Давление	КЭМ	Элементы	SFE	SFEDELE	SFELIST	SFSCALE	SFGRAD SFBEAM SFFUN SFCUM
Температура, обтекание	Твердотельная	Точки	BFK	BFKDELE	BFKLIST	BFTRAN	-
Температура, обтекание	Твердотельная	Линии	BFL	BFLDELE	BFLLIST	BFTRAN	-
Температура, обтекание	Твердотельная	Поверхности	BFA	BFADELE	BFALIST	BFTRAN	-
Температура, обтекание	Твердотельная	Объемы	BFV	BFVDELE	BFVLIST	BFTRAN	-
Температура, обтекание	КЭМ	Узлы	BF	BFDELE	BFLIST	BFSCALE	BFCUM
Температура, обтекание	КЭМ	Элементы	BFE	BFEDELE	BFELIST	BFSCALE	BFCUM
Инерционные	-	-	ASEL OMEGA DOMEGA CGLOG CGOMGA DCGOM	-	-	-	-

Приложение нагрузок с использованием интерфейса
Все операции с нагрузками, за исключением печати выбираются с использованием каскада меню. В меню «решение» вы выбираете «операции» (Apply, Delete и т.

д,) и затем объект, к которому вы прикладываете нагрузку (точка, линия, и т. д.).
Например, приложить нагрузки от перемещения к линии можно следующим образом: Main Menu > Solution> Load-Apply>Structural-Displasement> On Lines
Печать нагрузок
Для распечатки существующих нагрузок используйте:
Utility Menu>List>Loads>Load type
4. Выбор опций шагов нагружения.
Опции для гармонического анализа приведены в таблице 2.4.
Опции шагов нагружения Таблица 2.4

Опция	Команда	Интерфейс
Основные опции
Число гармоник в решении	NSUBST	Main Menu > Solution> Load Step Opt>Time/Friquens>Freq & Substep
Пошаговое или плавное нагружение (Step или ramped)	KBC	Main Menu > Solution> Load Step Opt>Time/Friquens>Time & Time Step/Freq & Substep
Опции динамики
Частотный диапазон силы	HARFRQ	Main Menu > Solution> Load Step Opt>Time/Friquens>Freq & Substep
Демпфирование	ALPHAD BETAD DMPRAT	Main Menu > Solution> Load Step Opt>Time/Friquens>Damping
Опции представления результатов
Печать	OUTPR	Main Menu > Solution> Load Step Opt>Output Ctrls>Solu Printout
База данных и результирующий файл	OUTRES	Main Menu > Solution> Load Step Opt>Output Ctrls>DB/Result File
Экстраполяция результатов	ERESX	Main Menu > Solution> Load Step Opt>Output Ctrls>Integration Pt

Основные опции включают следующее:

Число гармоник решения [NSUBST],

Вы можете запросить некоторое число гармоник в решении. Решение (шаги) будут размещены внутри выбранного частотного интервала [HARFRQ]. Например, если вы выберите 10 гармоник в диапазоне от 30 до 40 Гц, программа будет рассчитывать реакцию на 31, 32, 33,…39 и 40 Гц. Реакция не рассчитывается на нижней частоте диапазона.

Пошаговое или плавное нагружение [KBC].

Нагрузка может быть пошаговой или плавной. По умолчанию она плавная, это означает, что амплитуда нагрузки постепенно возрастает с каждым шагом.

Пошаговая нагрузка [KBS,1] означает, что амплитуда нагрузки будет поддерживаться постоянной для всех шагов в частотном диапазоне.

Частотный диапазон сил [HARFRQ].

Частотный диапазон должен быть определен в количестве циклов в единицу времени. Внутри этого диапазона вы затем можете выбрать число гармоник, которое будет рассчитано.

Демпфирование.

Демпфирование в системе должно быть обязательно определено, иначе может получиться бесконечная амплитуда на резонансной частоте. Частотно-зависимые коэффициенты демпфирования вводятся командами ALPHAD (пропорциональные матрице масс) и BETAD (пропорциональные матрице жесткости), а частотно-независимый коэффициент демпфирования вводится командой DMPRAT.
Замечание: если демпфирование не определено в прямом методе гармонического анализа, программа использует нулевое демпфирование.
Опции представления результатов включают следующее:

Вывод печати [OUTPR] использование этой опции позволяет включать различные данные результата в выходной файл (Jobname.OUT).
База данных и данные в результирующем выходном файле [OUTRES]. Эта опция контролирует данные в выходном файле (Jobname.RST).
Экстраполяция результатов [ERESX]. Использование этой опции позволяет просматривать результаты на элементах копированием их на узлы вместо экстраполяции (по умолчанию).

5.     Сохраните копию базы данных в файле с именем. Вы затем можете заново вызвать вашу модель, перезапустив ANSYS и вводя команду RESUME.
Команда SAVE. Интерфейс: Utility Menu>File>Save as.
6.     Запуск решения. Команда SOLVE. Интерфейс Main Menu>Solution>Solve – Current LS.
7.     Повторите шаги с 3 по 6 при других дополнительных нагрузках и других частотных диапазонах. Если вы планируете проводить постпроцессорную обработку (POST26), частотные диапазоны не должны перекрываться между шагами нагрузки. Другой метод увеличения шагов нагрузки заключается в сохранении шагов нагрузки в файле, и затем получении решения, используя макрос.

8.     Выйдите из режима решения.
2.2. Просмотр результатов.
Результаты гармонического анализа записываются в файл результатов Jobname.RST    Они состоят из следующих данных, каждый из которых зависит от частоты, для которой было получено решение:

Прямые данные.
Перемещения узлов (UX, UY, UZ, ROTX, ROTY, ROTZ).
Производные данные:
Напряжения в узлах и элементах;
Деформации в узлах и элементах;
Силы в элементах;
Реакции в узлах и т. д.

Если вы определили демпфирование в системе, ее реакция не будет находиться в одной фазе с действующими силами. Результаты расчетов будут комплексными числами и хранятся в виде действительных и мнимых частей. Комплексные результаты будут получаться, если к системе приложено несколько сил, отличающихся по фазам.
2.3. Постпроцессоры.
Вы можете просмотреть результаты, используя или постпроцессор POST26 или POST1. Обычно вначале используют POST26 для идентификации частот, при которых будут максимальные перемещения (или напряжения), выбирают наиболее интересные точки модели и затем используют POST1 для исследования объектов модели в этих критических режимах.

POST1 используется для просмотра результатов в объектах модели при некоторых частотах;
POST26 позволяет вам просматривать результаты в некоторых точках модели при некоторых частотных диапазонах.

Некоторые типичные операции постпроцессоров для гармонического анализа приведены ниже. Необходимо помнить, что:

Для просмотра результатов в POST1 и POST26 база данных должна содержать туже самую модель, для которой получено решение;
Должен быть получен результирующий файл (Jobname.RST).

Использование POST26
Результатом работы POST26 является таблица. Каждая переменная имеет свой ссылочный номер, первый номер зарезервирован для частоты.
1. Определите переменные, используя эти опции:
Команды:
NSOL для перемещений узлов;
ESOL для решений в элементах (например, напряжений)
RFORSE для реакций (сил).
Интерфейс:
Main Menu>TimeHist Postpro >Define Variables.

Команда FORSE позволяет вам определить полные силы, статические компоненты в полных силах, силы демпфирования, или инерционные компоненты.
2.     Рисование графика переменных в функции частоты или другой переменной. Введите команду PLCPLX для работы с амплитудой, фазовым углом, действительной или мнимой частью.
Команды: PLVAR, PLCPLX
Интерфейс:
Main Menu>TimeHist Postpro >Graph Variables.
Main Menu>TimeHist Postpro >Setting>Graph.
3.     Вывод на печать переменных. Для вывода экстремальных значений используйте команду EXTREM, затем введите команду PRCPLX для амплитуды, фазового угла, действительной или мнимой части.
Команды: PRVAR, EXTREM, PRCPLX.
Интерфейс:
Main Menu>TimeHist Postpro >List Variables/List Extremes
Main Menu>TimeHist Postpro >Setting>List.
В POST26 имеется много других функций, таких как математические преобразования над переменными с комплексной арифметикой, перемещение переменных в массивы и т. д.
В результате просмотра результатов вы можете определить критические частоты для дальнейшего использования постпроцессора POST1.
Использование POST1
1.     Прочитайте результат гармонического анализа. Для этих целей вы можете использовать команду SET, но при этом будет читаться либо действительная часть решения, либо мнимая. Истинная величина результата получится при применении команды SRSS (квадратный корень из суммы квадратов) действительной и мнимой частей.
2.     Нарисуйте деформированное состояние системы, контуры напряжений, деформаций и т. д. Или в векторном виде [PLVEC]. Для получения табулированного листинга используйте команды PRNSOL, PRESOL, и т.д.
Опция рисования деформированного состояния
Команда PLDISP
Интерфейс: Main Menu>General Postproc>Plot Results>Deformed Shape
Опция рисование контуров.
Команды: PLNSOL или PLESOL.
Интерфейс: Main Menu>General Postproc>Plot Results>Contour Plot-Nodal Solu или Element Solu.

Используйте опции для вывода результатов, таких как напряжение (SX, SY, SZ….), деформации (EPELX, EPELY, EPELZ…) и перемещения (UX, UY, UZ…).
Опция рисования в векторном виде.
Команда PLVEC
Интерфейс:
Main Menu>General Postproc>Plot Results>Vector Plot- Predefined.
Опция табулированный листинг.
Команды:
PRNSOL (результаты узлов)
PRESOL (результаты элементов)
PRRSOL (реакции)
NSORT, ESORT.
Интерфейс Main Menu>General Postproc>List Results>Nodal Solution.
Main Menu>General Postproc>List Results>Element Solution.
Main Menu>General Postproc>List Results>Reaction Solution.
Для сортировки данных перед печатью используйте команды NSORT или ESORT.
Постпроцессор POST1 имеет много других функций, таких как масштабирование результатов, преобразование результатов в различные координатные системы, комбинирование случаев нагружения и т. д.
2.4.         Гармонический анализ простой системы.
В этой простой задаче мы определим гармоническую реакцию двух массовой системы. Определим амплитуды Xi и фазовые углы fi для каждой массы mi. Система находится под действием гармонической силы

,
действующая на массу m1.
Свойства материалов для данной задачи

Амплитуда силы

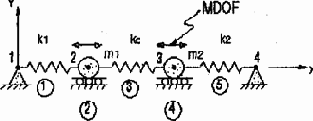Длина пружин является произвольной и используется только для определения направления деформации пружин. Две главные степени свободы определены на массах в направлении деформации пружин. Частотный диапазон выбран от нуля до 7.5 Гц. Всего учитывается 30 гармоник. Шаг по частоте составляет 7.5/30=0.25 Гц
Ввод заголовка задачи.
1.     Utility Menu>File>Change Title
2.     Введите текст «Harmonic Response of Two Mass Spring System» и нажмите «OK»
Определение типов элементов.
1.     Main Menu > Preprocessor>Element Type>Add/Edit/Delete.
2.     Нажмите Add. Появится диалоговая «коробка» типов элементов.
3.     Прочитайте список элементов в левой части «коробки» и выберите «Combination».

4.     Щелкните один раз в правой части коробки на «Spring-damper 14».
5.     Нажмите APPLY.
6.     В левой части выберите «Structural Mass» и выберите их.
7.     Щелкните один раз мышкой по «3D mass 21» в правой части «коробки».
8.     Нажмите ОК диалоговая «коробка» типов элементов закроется.
9.     Нажмите на «Close».
Ввод реальных констант.
1.     Main Menu > Preprocessor>Real Constants
2.     Нажмите Add. Откроется диалоговая коробка реальных констант.
3.     Нажмите Type 1.
4.     Нажмите ОК. Откроется диалоговая «коробка» для Combin14.
5.     Введите 200 для жесткости пружин (К) и 0.1 для коэффициента демпфирования (CV1) и нажмите ОК.
6.     Повторите шаги 2-4 для типа элемента 2, MASS21.
7.     Введите 0.5 для для массы в направлении X и нажмите ОК.
8.     Нажмите Close, закройте коробку реальных констант.
Построение узлов.
1.     Main Menu > Preprocessor>Modeling-Create>Nodes>In Active CS.
2.     Введите 1 для номера узла.
3.     Введите 0, 0, 0 для координат X, Y, Z соответственно.
4.     Нажмите Apply.
5.     Введите 4 для номера узла.
6.     Введите 1, 0, 0 для координат X, Y, Z соответственно.
7.     Нажмите ОК.
8.     Utility Menu>PlotCtrl>Numbering. Откроется коробка управления нумерацией.
9.     Нажмите один раз «Node Numbers on»
10.            Нажмите ОК.
11.            Main Menu > Preprocessor>Modeling-Create>Nodes>Fill between Nds

12.            В графическом окне нажмите на узлы 1 и 4 (в левой и правой стороне экрана). Маленькая «коробка» откроется вокруг каждого узла.
13.            Нажмите ОК. Откроется диалоговая коробка построения узлов между двумя узлами.
14.            По умолчанию строится 2 узла. Нажмите ОК. Узлы 2 и 3 появятся на графическом окне.
Построение элементов пружин.
1.           Main Menu > Preprocessor>Modeling-Create>Elements>Auto Numbered-Thru Nodes. Откроется “пиковое” меню.
2.           На графическом окне нажмите один раз на узлы 1 и 2.
3.           Нажмите Apply. Появится линия между выбранными узлами.
4.           Нажмите один раз на узлы 2 и 3.
5.           Нажмите Apply. Появится линия между выбранными узлами.
6.           Нажмите один раз на узлы 3 и 4
7.           Нажмите ОК. Появится линия между выбранными узлами.
Построение элементов масс
1.           Main Menu>Preprocessor>Modeling-Create>Elements>Elem Attributes
2.           Введите 2 как номер типа элемента.
3.           Введите 2 как номер реальных констант и нажмите ОК.
4.           Main Menu > Preprocessor>Modeling-Create>Elements>Auto Numbered-Thru Nodes. Откроется “пиковое” меню.
5.           На графическом окне нажмите один раз на узел 2.

6.           Нажмите Apply.
7.           На графическом окне нажмите один раз на узел 3 нажмите ОК.
Выбор типа анализа, главных степеней свободы и шагов нагрузки.
1.     Main Menu > Solution> Analysis Type- New Analys
2.     Нажмите на «Harmonic» и нажать ОК.
3.     Main Menu > Solution> Analysis Option
4.     Нажмите на Full, выбирая метод решения.
5.     Нажмите один раз на “Amplitude+phase» для выбора формата вывода.
6.     Нажмите ОК на диалоговом ящике Full Harmonic Analyze
7.     Main Menu > Solution> Load Step Opt> -Output Ctrls>SoluPrintout.
8.     Нажмите на «Last substep» для печати частот нажать на ОК.
9.     Main Menu > Solution> Load Step Opt>Time/Friquens>Freq & Substep
10.            Введите 0 и 7.5 для частотного диапазона.
11.            Введите 30 для числа шагов.
12.            Нажмите на «Stepped»
13.            Нажмите ОК.
Определение нагрузок и граничных условий.
1.      Main Menu > Solution> Load-Apply>Structural-Displasement>On Nodes
2.      Нажмите «Pick All» «Выбрать все»
3.      Выбрать UY.
4.      Нажать ОК.
5.      Main Menu > Solution> Load-Apply>Structural-Displasement>On Nodes
6.      В графическом окне нажать на узлы 1 и 4.
7.      Нажать ОК.
8.      В диалоговом окне нажать на UX и UY.

9.      Нажать на ОК.
10. Main Menu > Solution> Load-Apply>Structural-Force/Moment>On Nodes
11. В графическом окне нажать на узел 2.
12. Нажать ОК.
13. В диалоговом окне выбрать FX
14. Ввести 200 для действительной части и нажать ОК.
Решение модели.
1.     Main Menu>Solution>Solve – Current LS.
2.     Посмотреть информацию в окне статуса и нажать Close.
3.     Нажать ОК.
4.     Когда решение закончится, появится диалоговое окно «Solution is done” Нажать Close.
Просмотр результатов.
Для этого примера мы будем просматривать результаты решения для узлов 2 и 3.
1.     Определение списка переменных для вывода: Main Menu>TimeHist Postpro >Define Variables. Откроется диалоговое окно.
2.     Нажать Add. Откроется диалоговое окно.
3.     По умолчанию выбираются узловые решения «Nodal DOF». Откроется диалоговое окно узловых перемещений.
4.     Ввести 2, как номер переменной. (Номер 1 по умолчанию – частота).
5.     Ввести 2, как номер узла.
6.     Ввести 2UX, как метку пользователя. (На графике соответствующая кривая выведется с этой меткой).
7.     В правой части «коробки» найти «Translation UX»
8.     Нажать ОК.
9.     Нажать «Add» на диалоговом окне выбора переменных. Откроется диалоговое окно.
10.            Нажать ОК на узловые решения «Nodal DOF». Откроется диалоговое окно.
11.            Введите 3 как номер переменной.
12.            Введите 3 как номер узла
13.            Введите 3UX, как метку пользователя.
14.            В правой части «коробки» найти «Translation UX»

15.            Нажать ОК.
16.            Нажать Close
17.            Оформление графика Utility Menu>PlotCtrl>Style>Graphs Откроется меню управления графиками
18.            В диалоговом окне для типа сетки выбрать X и Y.
19.            Нажать ОК.
20.            Вывод графика Main Menu>TimeHist Postpro >Graph Variables.
21.            Введите 2 как 1-ю переменную графика.
22.            Введите 3 как 2-ю переменную графика.
23.            Нажать ОК. Появится график (рис.2.2).

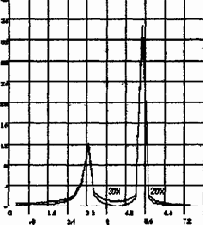Рис.2.2
3.     Усеченный метод
Усеченный метод использует усеченные матрицы для гармонического расчета. Решение задачи состоит из следующих шагов:
1.     Построение модели;
2.     Приложение нагрузок и получение усеченного решения;
3.     Просмотр результатов усеченного решения.
4.     Расширение решения
5.     Просмотр результатов расширенного решения.
Первый шаг конечно, точно такой же, как и для полной модели.
3.1.         Приложение нагрузок и получение усеченного решения.
В усеченном методе мы подразумеваем главные степени свободы.
1.     Введите процессор решения.
Команда /SOLU Интерфейс: Main menu>Solution
2.     Определите тип анализа и опции. Опции для усеченного анализа те же самые, как для полного метода.

Выберите усеченный метод решения;
Вы можете включить эффекты предварительного напряжения [PSTRES].

Это требует файлов элементов с предшествующего статического или переходного динамического анализа.

3. Определите главные степени свободы. Главные степени свободы являются определяющими или динамическими степенями свободы, определяющими динамическое поведение системы. Для усеченного динамического анализа главные степени свободы выбираются с учетом места на системе, где вы хотите приложить силы или не нулевые перемещения.
4. Приложите нагрузку на модель. Гармоническая нагрузка может быть той же самой, что описана для полного метода, исключая некоторые особенности:

Допускается приложение только сил и перемещений. Нагрузки элементов, такие как давление, температура, ускорение не поддерживаются.
Силы и ненулевые перемещения должны быть приложены только к главным степеням свободы.

5.     Выберите опции шагов нагрузок. Они те же самые, что для полного метода, за исключением команд OUTRES и ERESX. Команда OUTPR контролирует вывод на печать узловые решения главных степеней свободы. [OUTPR, NSOL, ALL (или NONE)].
6.     Сохраните копию базы данных.
Utility Menu>File>Save as.
7.     Запустите решение
Main Menu>Solution>Solve – Current LS.
8.     Повторите шаги с 4 по 7 при дополнительных силах и частотных диапазонах. Если вы планируете использовать временной частотный постпроцессор POST26, частотные диапазоны не должны перекрываться.
9.     Закройте меню SOLUTION.
3.2            Просмотр результатов усеченного решения.
Результаты усеченного гармонического анализа записываются в усеченный файл перемещений Jobname. RFRQ. Он состоит из перемещений по главным степеням свободы, которые имеют гармонический характер для каждой частоты силы, для которых было получено решение. Как и для полного метода, эти перемещения будут комплексными, если было определено демпфирование, или если силы были приложены не в одной фазе.

Вы можете просмотреть перемещения по главным степеням свободы в функции от частоты, используя POST26. ( POST1 не может быть использован, потому что полное решение по всем степеням свободы не получено). Процедура использования POST26 точно такая же, как и для полного метода, исключая некоторые особенности.

Перед определением переменных для POST26 используйте команду FILE для выбора данных, которые будут читаться из файла Jobname.RFRQ. Например, если HARMONIC - имя задачи команда будет иметь вид: FILE, HARMONIC,RFRQ.
Учитываются только данные о степенях свободы узлов (соответствующие главным степеням свободы), таким образом, применяется только команда NSOL для определения переменных.

3.3. Расширение решения
Расширение решения предназначено для расчета полных перемещений, напряжений и сил для всех степеней свободы. Эти расчеты проводятся только для частот и фазовых углов, которые вы выбрали. Перед началом решения расширения вы должны просмотреть усеченного сечения, используя POST26 и идентифицировать критичные частоты и фазовые углы.
Расширение решения требуется не всегда. Например, если вы интересуетесь в основном перемещениями в специфических точках конструкции, усеченное решение может удовлетворить ваши запросы. Если вы хотите определить перемещения не по главным степеням свободы, или вас интересуют напряжения, вы должны применить расширенное решение.
Необходимо помнить, что:

Должны быть созданы файлы RFRQ, TRI, EMAT и ESAV;
База данных должна содержать ту же самую модель, для которой получено усеченное сечение.

3.3.1. Расширение мод
1. Перезапустите процессор решения
/SOLU
Main Menu > Solution.
2. Активизируйте решение расширения и его опции.

Опции	Команды	Интерфейс
Расшиение Вкл/Выкл	EXPASS	Main Menu>Solution>Analys Type-Expansion Pass
Число решений для расширения	NUME XP	Main Menu>Solution>Load Step Opt-Expansion Pass>Range of Solu s
Частотный диапазон для расширения	NUME XP	Main Menu>Solution>Load Step Opt-Expansion Pass>Range of Solu s
Фазовый угол для расширения	HREXP	Main Menu>Solution>Load Step Opt-Expansion Pass>Range of Solu s
Расчет напряжений Вкл/выкл	NUME XP EXPSOL	Main Menu>Solution>Load Step Opt-Expansion Pass>Range of Solu s
Узловые решения Формат вывода	HROUT	Main Menu>Solution>Analys Opt

Опция Expansion Pass On/Off [EXPASS] (Расширение Вкл/Выкл)
Выберите ON
Опция Число решений для расширения [NUMEXP, NUM].
Выберите число. Это число равномерно распределенных решений в частотном диапазоне. Например, команда NUMEXP ,4,1000,2000 выбирает 4 решения в частотном диапазоне от 1000 до 2000 Гц при 1250, 1500, 1750, 2000 Гц.
Опция Частотный диапазон для расширения [NUMEXP, BEGRNG, ENDRNG].
3. Выберите частотный диапазон. (См. предыдущий пример). Если вы не хотите расширять несколько решений, вы можете использовать команду EXPSOL для идентификации единственного решения для расширения (или с помощью задания номера шага нагрузки, или с помощью его частоты). Если несколько решений будет расширено в некотором частотном диапазоне, мы предполагаем, что вы запросите и действительную и мнимую части в полученном расширении [HREXP, ALL]. Таким образом, вы можете легко комбинировать две части в POST26 для просмотра пиковых значений перемещений, напряжений и других результатов. С другой стороны, для единственного решения, полученного командой [EXPSOL], вы можете выбрать фазовый угол. В этом случае пиковое перемещение может быть получено с использованием команды [HREXP,angle].
Опция вычисление напряжений Вкл/Выкл.[NUMEXP или EXPSOL].
Вы можете выключить вычисление напряжений и сил, если захотите. По умолчанию они вычисляются.
Опция формат вывода узловых решений [HROUT].
Определите, как гармонические перемещения будут выводиться на печать (Jobname. OUT). Вы можете выбрать в виде действительной и мнимой части (по умолчанию) и виде амплитуды и фазового угла
Команда OUTPR. Интерфейс: Main Menu>Solutions>Load Step Opt-Output Ctrls>Solu Printout.
База данных и результирующий выходной файл
Используются следующие опции для управления данными в результирующем выходном файле (Jobname. RST).
Команда OUTRES. Main Menu>Load Step Opt-Output Ctrls>DB/Results File.
Экстраполяция результатов.
Используя эти опции можно просмотреть интегральные результаты для элементов путем копирования их в узлы вместо экстраполяции (по умолчанию).

Примечание: Поле FREQ команды OUTPR и OUTRES может иметь два значения: ALL или NONE.
Команда ERESX. Интерфейс: Main Menu>Load Step Opt-Output Ctrls>Integration Pt.
4.              Запустите решение расширения.
Main Menu>Solution>Solve – Current LS.
5.              Повторите шаги 2,3 и 4 при дополнительных решениях. Каждое решение расширения хранится как отдельный шаг нагрузки в файле результатов.
6.              Выйдите из режима решения, закрыв меню Solution.

3.3.2. Просмотр результатов расширения
Результаты расширенного решения записываются в файл Jobname.RST. Он состоит из следующих данных, рассчитанных для каждой частоты, для которой было получено решение.

Прямые данные:
Перемещения узлов (UX, UY, UZ, ROTX, ROTY, ROTZ).
Производные данные:
Напряжения в узлах и элементах;
Деформации в узлах и элементах;
Силы в элементах;
Реакции в узлах;
И т.д.

Вы можете просмотреть их, используя POST1. Если вы провели расширение решения на нескольких частотах, вы можете использовать POST26 для получения графика напряжений в функции от частоты.
Процедура использования POST1 или POST26 та же самая, что описана для полного метода, исключая одну особенность: если вам требуется фазовый угол [HREXP, angle], то только одно решение возможно для каждой частоты.
4.       Метод суперпозиции мод
Метод суперпозиции мод основан на суммировании коэффициентов собственных мод, полученных в модальном анализе для расчета гармонической реакции. Процедура использования метода состоит из следующих основных шагов:
1.     Построение модели;
2.     Решение задачи на собственные частоты и формы (модальный анализ);
3.     Получение гармонической реакции методом суперпозиции мод;
4.     Расширение полученного решения;

5.     Просмотр результатов.
Некоторые замечания по модальному анализу

Подходят следующие методы: подпространства (subspace), блочный (Block Lanczos), усеченный (reduced) или Power Dynamic. (Другие методы, такие как несимметричный и демпфированный не применяются для суперпозиции мод). Если применяется метод Power Dynamic для модального анализа, то возможно применение не нулевых нагрузок или перемещений.
Модальный анализ должен содержать столько мод, сколько необходимо для получения гармонической реакции.
При использовании усеченного метода включите те главные степени свободы, к которым были приложены гармонические нагрузки;
Если вам необходимо гармонически изменяющиеся нагрузки на элементы (давление, температура, ускорения), вы должны выбрать их в модальном анализе. Нагрузки игнорируются в модальном анализе, но вектор нагрузок будет рассчитан и записан в файле собственных форм (Jobname.MODE). Вы можете использовать вектор нагрузок в гармоническом решении.
Раскрытие собственных мод не обязательно для метода суперпозиции. (если вы хотите посмотреть формы мод графически, для этого нужно их расширение);
Данные модели, такие как повороты узлов не должны изменяться между модальным и гармоническим анализом.

4.1.         Решение задачи гармонического анализа методом суперпозиции мод.
В этом шаге программа использует формы мод, полученные в модальном анализе. Файл собственных мод (Jobname.MOD) должен быть создан и база данных должна содержать ту же самую модель, для которой был проведен модальный анализ. Если при модальном анализе использовался метод подпространства, или блочный метод, и при этом использовалась матрица масс по умолчанию, т. е. не диагональная матрица масс, может быть получен полный файл (Jobname. FULL).
1.     Войдите в режим решения.
/SOLU или Main Menu>Solution
2.     Определите тип анализа и его опции. Это тоже самое, что описано для полного метода ,исключая некоторые различия.

Выберите метод суперпозиции мод [HROPT].
Выберите моды, которые вы хотите использовать для решения [HROPT]. Это определяет точность гармонического решения. Обычно число мод должно быть выбрано так, чтобы их частотный диапазон был больше на 50%, чем частотный диапазон приложенных сил.
Обычно решение «сгущается» около собственных частот конструкции [HROUT] для получения более точной кривой реакции.
Обычно на каждой частоте печатается суммарная таблица коэффициентов вклада каждой моды в общую реакцию системы. [HROUT].

3. Приложите нагрузки к модели. Гармоническое нагружение то же самое, исключая следующие особенности:

Только силы, ускорения и вектор нагрузок, созданный в модальном анализе являются правильными. Используйте команду LVSCALE для приложения вектора нагрузок из модального анализа.
Если используются моды, полученные усеченным методом модального анализа, силы должны быть приложены к главным степеням свободы.

4.     Выберите опции шагов нагрузки. Это то же самое, что описано для усеченного метода, исключая то, что вы можете выбрать модальное демпфирование [MDAMP]. С помощью команды [NSUBST] вы можете выбрать число решений с каждой стороны резонансного пика, если выбрана опция [HROUT]. По умолчанию вычисляется 4 решения, но вы можете выбрать другое число от 2 до 10.
5.     Если вы использовали метод подпространства или блочный метод, вы можете использовать узловые компоненты с помощью команды OUTRES, NSOL для ограничения данных перемещения в редуцированный файл перемещений Jobname.RFRQ. Решение задачи о расширении будет давать правильные результаты для тех узлов и тех элементов, в которых все узлы элементов записаны в файл с расширением RFRQ.
6.     Сохраните копию базы данных.
Utility Menu>File>Save as.
7.     Запуск задачи на решение.
Main Menu>Solution>Solve – Current LS.
8.     Повторите шаги с 3 по 6 при дополнительных нагрузках и частотных диапазонах.

Если вы планируете использовать временной частотный постпроцессор POST26, частотные диапазоны не должны перекрываться.
9.     Выйдите из режима решения.
4.2.         Расширение решения и просмотр результатов
Процедура расширения решения та же самая, что описана для усеченного метода. Файл Jobname.TRI необходим, только если использовался метод раскрытия редуцированных мод. Результаты состоят из гармонически изменяющихся перемещений, напряжений и усилий реакции для каждой частоты. Вы можете просмотреть эти результаты, используя POST26 или POST1
5.      Гармонический анализ предварительно напряженных конструкций.
Гармонический анализ предварительно напряженных конструкций рассчитывает гармоническую реакцию таких систем, как скрипичная струна. Это возможно только при усеченном методе решения или методе суперпозиции мод. Принимается, что амплитуда гармонической составляющей напряжения намного меньше, чем величина предварительного напряжения.
Процедура редуцированного решения предварительно напряженной конструкции та же самая, что для любого редуцированного анализа, исключая то, что вначале необходимо провести статический анализ.
1.     Постройте модель и получите статический расчет с учетом эффекта предварительного нагружения. [PSTRES, ON].
2.     Перезапустите «SOLUTION» и получите редуцированное гармоническое решение с включением эффектов предварительного нагружения. [PSTRES, ON]. При этом должны быть получены файлы Jobname.EMAT и Jobname.ESAV из статического анализа.
3.     Для учета эффекта предварительного нагружения по методу суперпозиции мод вы должны вначале выполнить модальный анализ с учетом предварительного напряжения. Результаты этого анализа будут учитываться в методе суперпозиции мод.
6.      АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ
6.1.         Введение.

Анализ переходных процессов ( иногда называемый анализом во времени) предназначен для нахождения динамической реакции системы при действии некоторых нагрузок, зависящих от времени. Вы можете использовать этот тип анализа для определения временной зависимости перемещений, деформаций, напряжений и сил в системе как реакцию на некоторую комбинацию статических, переходных и гармонических сил. Расчет во временной шкале означает, что эффекты инерции и демпфирования являются важными. Если эти эффекты не учитываются, то достаточно статического анализа.
Основное уравнение движения имеет вид

,
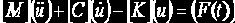
где

-матрица масс,

-матрица демпфирования,

-матрица жесткости, (

)-вектор ускорений узлов,

-вектор скоростей узлов,

-вектор перемещений узлов.

-вектор нагрузки.
В некоторый данный момент времени t это уравнение может интерпретироваться как набор «статических» уравнений равновесия с учетом сил инерции и сил демпфирования. ANSYS использует метод Нъюмарка в процедуре интегрирования по времени. Приращение по времени задается временными шагами.
6.2.         Подготовка для проведения динамического анализа переходных процессов.
Вы будете использовать тот же самый набор команд для построения модели и получения динамического анализа переходных процессов, что вы используете для других типов конечно-элементного анализа. Динамический анализ переходных процессов более трудоемкий, чем статический анализ и требует больших ресурсов компьютера и очень больших ваших «инженерных» ресурсов (например, затраченного времени). Вы можете сберечь часть этих ресурсов проведением некоторой предварительной работы для понимания физической сущности задачи. Например, вы можете:
1.     Вначале решить простейшую задачу. Модель, состоящая из балок, масс и пружин может давать хорошее приближение к истинному решению при минимальных затратах времени. Эта простейшая модель может полностью удовлетворить вас при решении задачи отыскания динамической реакции системы.

2.     Если вы включаете в систему нелинейности, попытайтесь вначале понять, как эти эффекты влияют на систему при статической нагрузке. В некоторых случаях их не имеет смысла включать в динамический анализ.
3.     Попытайтесь понять динамику системы. Для этого полезно провести модальный анализ для определения собственных частот и мод колебаний. Это поможет вам понять реакцию системы при действии нагрузок. Кроме того, знание собственных частот поможет вам определить правильный размер временных шагов.
4.     Для нелинейных задач используйте технологию подсистем (substructuring) линейной части модели для сокращения времени решения.
6.3. Три метода решения.
Существует три метода решения задачи динамического анализа переходных процессов: полный, редуцированный и метод суперпозиции мод. Программа ANSYS/LINEAR PLUS позволяет только метод суперпозиции мод. Перед подробным изучением каждого из этих методов рассмотрим достоинства и недостатки каждого из них.
6.3.1. Полный метод.
Полный метод использует полные системы матриц для отыскания динамической реакции системы. Он является наиболее мощным из трех методов, потому что он позволяет учитывать все типы нелинейностей (пластичность, большие перемещения, большие деформации и т. д.). Если вы не хотите учитывать нелинейности, вы должны рассмотреть целесообразность применения двух других методов, так как полный метод – наиболее «дорогой» из этих трех методов.
Преимущества полного метода:

Он наиболее простой, так как не требует выбора главных степеней свободы или формы мод.
Он позволяет учитывать все типы нелинейностей.
Он использует полные матрицы, так что аппроксимация матрицы масс не требуется.
Все перемещения и напряжения определяются в одном шаге.
Он учитывает все типы нагрузок: узловые силы, не нулевые перемещения (хотя это не рекомендуется), нагрузки элементов (давление и температура).
Он позволяет эффективно использовать твердотельные нагрузки.

Основной недостаток полного метода заключается в том, что он требует больших ресурсов памяти и большого времени решения.

6.3.2. Редуцированный метод.
Редуцированный метод конденсирует размер задачи путем использования главных степеней свободы и редуцированных матриц. После расчета перемещений по главным степеням свободы, ANSYS расширяет решение на полный набор степеней свободы. Преимущества редуцированного метода:

Он быстрее работает и является менее «дорогим» методом.

Недостатки редуцированного метода:

В начальном решении определяются только перемещения по главным степеням свободы. Второй шаг, известный как шаг расширения, необходим для получения всех перемещений, напряжений, сил. Иногда шаг расширения не требуется.
Нагрузки элементов (давление, температура) не поддерживаются, но допускаются ускорения.
Все нагрузки должны быть приложены к главным степеням свободы, выбранных пользователем. Это ограничивает применение твердотельных нагрузок.
Временные шаги должны быть постоянными, так как автоматическое определение величины шагов не поддерживается.
Допускаются нелинейности вида контактных условий между узлами или зазоры.

6.3.3. Метод суперпозиции мод.
В методе суперпозиции мод суммируются коэффициенты форм мод из модального анализа. Этот метод является единственно допустимым методом для программы ANSYS/LINEAR PLUS. Его преимущества:

Он работает быстрее и является менее «дорогим» методом по сравнению и с редуцированным и полным методами.
Нагрузки элементов, приложенные в модальном анализе, могут быть приложены с помощью команды LVSCALE.
Метод поддерживает модальное демпфирование (отношение демпфирования в функции от номера моды).

Недостатки метода:

Размер временного шага должен быть постоянным, так как автоматический выбор шага не поддерживается.
Допускаются нелинейности вида контактных условий между узлами или зазоры.
Он не может использоваться для «плавающей» или не закрепленной системы.
Когда вы используете программу Power Dynamics, начальные условия могут не иметь предварительно приложенных нагрузок или перемещений.
Метод не поддерживает применение не нулевых перемещений.

6.4 Динамический анализ переходных процессов полным методом.

Процедура решения задачи динамического анализа переходных процессов полным методом состоит из трех основных шагов:
1.     Построение модели;
2.     Приложение нагрузок и получение решения;
3.     Просмотр результатов.
Построение модели. На этом этапе вы определяете имя задачи, заголовок задачи затем, используя препроцессор, определяете тип элементов, реальные константы, свойства материалов и геометрию модели.

Вы можете использовать и линейные и нелинейные элементы;
Модуль упругости EX или жесткость в любой форме и плотность (DENS) или масса в некоторой форме должны быть заданы. Свойства материалов могут быть линейными или нелинейными, изотропными, ортотропными, или температурно-зависимыми.

Некоторые замечания по плотности разбиения.

Плотность разбиения должна быть достаточно тонкой, чтобы представить желаемую высшую формы моды;
Регионы модели, где вас интересуют напряжения и деформации, должны быть разбиты тоньше, чем регионы, где вас интересуют только перемещения;
Если вы хотите включить нелинейности, разбиение должно быть таким, чтобы проявлялся эффект от этих нелинейностей. Например, пластичность требует обоснованной плотности точек интегрирования (следовательно, тонкого разбиения) в поверхностях с высоким градиентом пластической деформации;
Если вас интересуют эффекты распространения волн, разбиение должно быть достаточным, для представления волны. Обычно требуется порядка 20 элементов на длину волны по направлению ее распространения.

Приложение нагрузок и получение решения. В этом шаге вы определяете тип анализа, и его опции, прикладываете нагрузки, выбираете опции шагов нагрузки и инициируете конечно-элементное решение.
1. Войдите в режим «решение» командой /SOLU или через интерфейс:
Main Menu > Solution
2. Определите тип анализа и его опции (табл. 6.1).
Таблица 6.1

Опции	Команда	Действия в интерфейсе
New Analysis	ANTYPE	Main Menu > Solution> Analysis Type- New Analys
Analysis Type: Transient Dynamic	ANTYPE	Main Menu > Solution> Analysis Type- New Analys>Transient Dynamic
Метод решения	TR NOPT	Main Menu > Solution> Analysis Option
Вид матрицы масс	LUMPM	Main Menu > Solution> Analysis Option
Эффект больших деформаций	NLGEOM	Main Menu > Solution> Analysis Option
Эффект упрочнения	SSTIF	Main Menu > Solution> Analysis Option
Опции Ньютона-Рафсона	NROPT	Main Menu > Solution> Analysis Option
Программа решения	EQSLV	Main Menu > Solution> Analysis Option

Каждая из этих опций будет подробно рассмотрена ниже.
Опция New Analysis [ANTYPE]. Эта опция позволяет заново анализировать задачу. Применение этой опции необходимо, если а) вы хотите предварительно придать системе предварительное статическое напряжение или для полного анализа переходных процессов вы хотите расширить временные пределы. Б) Вы хотите перезапустить задачу с учетом нелинейностей. Файлы Jobname. EMAT, Jobname.ESAV, Jobname. DB из первоначального решения должны быть готовы для рестарта. Результаты будут помещены в файл Jobname. RST.
Опция Analys Type [ANTYPE]
Выберите Transient Dynamic.
Опция Solution Method (Метод решения) [TRNOPT].
Выберите full (по умолчанию), редуцированный (reduсed) или метод суперпозиции мод (mode superposition method).
Опция Mass Matrix Formulation (вид матрицы масс) [LUMPM]
Эту опцию мы рекомендуем принимать по умолчанию. Для некоторых задач, использующих “тонкие” системы, такие, как тонкие балки или очень тонкие оболочки аппроксимация матрицы масс с помощью сосредоточенных масс часто приводит к лучшим результатам. Аппроксимация матрицы масс при помощи сосредоточенных масс требует меньшего времени решения и памяти.
Опция Large Deformation Effects (Эффект больших деформаций) [NLGEOM]
Выберите «ON» только если вы учитываете большие перемещения (например, длинная тонкая балка под действием изгибающего момента) или большие деформации (например, как в задачах штамповки). Большие перемещения и большие деформации являются геометрически не линейными задачами. По умолчанию учитываются малые перемещения и малые деформации.
Опция Stress Stiffening Effects (Эффект упрочнения) [SSTIF]
Выберите «ON» в следующих ситуациях (по умолчанию эта опция включена, когда включен учет больших деформаций NLGEOM и SOLCONTROL):

Если при решении задачи с малыми перемещениями вы находите напряжения в системе при существенном увеличении (или снижении) ее жесткости, например тонкая круглая мембрана при действии нормального давления.
Если вам необходима помощь оценки сходимости при учете больших перемещений.

Опция Ньютона – Рафсона (Newton – Raphson) [NROPT].

Эта опция выбирается для представления тангенциальных матриц, получаемых в результате решения и используется, только если учитываются нелинейные эффекты. Выбираются опции, приведенные ниже:

Program – chosen (по умолчанию);
Полный (Full);
Модифицированный (Modified);
Начальной жесткости (Initial Stiffnes).

Опция метод решения (Equation Solver) [EQSLV].
Выберите одну из следующих методов:

Фронтальный метод (по умолчанию для линейных систем);
Метод соединенных градиентов Якоби (JCG);
Метод JCG out – of – memory;
Неполный метод соединенных градиентов Холецкого (ICCG);
Метод соединенных градиентов с предварительными условиями (PSG);
Метод PSG out- of –memory;
Итерационный (с автоматическим выбором; Для линейного статического / полного переходного анализа или пошагового переходного температурного анализа) – рекомендуется;
Разреженный (SPAR) (по умолчанию для нелинейного анализа когда включен режим SOLCONTROL)

Для больших моделей мы рекомендуем метод PSG.
3. Приложение нагрузки к модели.

Переходный анализ по определению использует нагрузки, зависящие от времени. Выбирая такие нагрузки, вам необходимо разделить кривые «нагрузка-время» на подходящие временные шаги. Каждый «угол» на временной кривой может быть как один шаг нагрузки, как показано на рис. 6.1.
Рис 6.1
Первый временной шаг обычно используется для установки начальных условий. Затем вы должны определить нагрузки и опции шагов нагрузки для последующих временных шагов. Для каждого временного шага вам необходимо определить величину нагрузки и значение времени, определить опции нагрузки, такие как величина скачка, или плавное нарастание нагрузки, использование автоматического выбора шага и т. д. Затем вы должны записать каждый временной шаг в файл и решать все временные шаги вместе.
Учет начальных условий.
Первый временной шаг в приложенной нагрузке используется для установки начальных условий, т. е. при t=0. Динамический анализ переходных процессов требует два набора начальных условий (так как уравнения движения представляют собой уравнения второго порядка): начальные перемещения

и начальные скорости

.

Если они не заданы, то они считаются равными нулю. Начальные ускорения

принимаются всегда равными нулю, но вы можете выбрать ненулевые начальные ускорения приложением соответствующих ускорений на малом временном интервале.
Нулевые начальные перемещения и нулевые начальные скорости - это начальные условия по умолчанию, т.е. если

вы не должны ничего определять. Вы можете приложить нагрузки, соответствующие первому «углу» кривой «нагрузка-время» в первом временном шаге.
Ненулевые начальные перемещения и ненулевые начальные скорости вы можете ввести такие начальные условия с помощью команды IC или через интерфейс:
Main Menu>Solution>-Loads Apply>Initial Condit`n>Define
Предостережение: Нельзя определять несовместные начальные условия. Например, вы определили начальную скорость в единственной степени свободы, а начальная скорость во всех других степенях свободы равна нулю, что приводит к конфликту начальных условий. В большинстве случаев начальные условия вводятся во всех незакрепленных степенях свободы модели. Если эти начальные условия не одинаковы для всех степеней свободы, то нужно вводить их, как показано ниже. (См. описание команд TIMIND и IC).
Нулевые начальные перемещения и ненулевые начальные скорости Ненулевые скорости вводятся приложением малых перемещений в течение малого временного интервала на части конструкции, где должна быть определена скорость. Например, если

, вы можете ввести перемещение равное 0,001 за временной интервал 0,004, как показано ниже.
TININT, OFF |Эффект временного интегрирования выключен
D, ALL, UY, 0.001 |Введены малые перемещения (скорость направлена по Y )
TIME, 0.004 | начальная скорость =0,001/0,004=0,25
LSWRITE | Запись данных в файл шагов нагрузки (Jobname.S01)
DDELE, ALL, UY| Уничтожение приложенных перемещений
TININT, ON |Эффект временного интегрирования включен
Ненулевые начальные перемещения и ненулевые начальные скорости
Это тот же случай, что приведен выше, исключая то, что вместо малых перемещений вводятся их действительные значения.

Например, если

, вы должны ввести перемещение равное 1,0 в течение временного интервала 0,4.
TININT, OFF |Эффект временного интегрирования выключен
D, ALL, UY, 1.0 |Введены перемещения (скорость направлена по Y )
TIME, 0.4 | начальная скорость =1.0/0,4=2,5
LSWRITE | Запись данных в файл шагов нагрузки (Jobname.S01)
DDELE, ALL, UY| Уничтожение приложенных перемещений
TININT, ON |Эффект временного интегрирования включен
Ненулевые начальные перемещения и нулевые начальные скорости
Это требует использования двух шагов [NSUBST,2] с шагом изменения выбранных перемещений [KBS,1]. Без шага изменения заданные перемещения будут изменяться непосредственно со временем, приводя к ненулевой начальной скорости. Пример, приведенный ниже, показывает, как ввести

.
TININT, OFF      |Эффект временного интегрирования выключен
D, ALL, UY, 1.0 |Введены перемещения (скорость направлена по Y )
TIME, 0.001 | Малый временной интервал
NSUBST, 2 |Два шага
KBC,1          | Скачек нагрузки
LSWRITE    | Запись данных в файл шагов нагрузки (Jobname.S01)
                  Анализ переходного процесса
TIMINT,ON | Эффект временного интегрирования включен
TIME,….   | Реальный временной шаг
DDELE, ALL, UY| Удаление заданных перемещений
KBC,0                   |Плавно возрастающая нагрузка (если нужно)
Продолжение процедуры нормального переходного анализа
Ненулевое начальное ускорение
Это может быть аппроксимировано выбором требуемого ускорения [ACEL] в малый интервал времени. Команды, применяемые для ввода начального ускорения 9,81, приведены ниже.
ACEL,,9.81 | Начальное ускорение в Y направлении
TIME, 0.001 | Малый временной интервал
NSUBST,2   | Два шага
KBS,1           |Скачек нагрузки
LSWRITE    | Запись данных в файл шагов нагрузки (Jobname.S01)
Переходный анализ
TIME,….| Реальный временной шаг
DDELE,..   | Удаление заданных перемещений (если требуется)
KBC,0     | Плавно возрастающая нагрузка (если нужно)
Продолжение процедуры нормального переходного анализа

Приложение нагрузок для динамического анализа переходных процессов
В таблице 6.2 приведены возможные нагрузки для динамического анализа переходных процессов. Выбирая инерционные нагрузки, вы можете определить их и для твердотельной модели, и для конечно-элементной модели. Вы можете также определить сложные граничные условия массивом табличного типа.
Таблица 6.2
Нагрузки для переходного анализа

Тип нагрузки	Категория	Команды	Интерфейс
Перемещения (UX, UY, UZ, ROTX, ROTY, ROTZ	Закрепления	D	Main Menu>Solutions>-Loads-Apply-Stuctural-Displasiment
Силы, моменты (FX, FY, FZ, MX, MY, MZ)	Силы	F	Main Menu>Solutions>-Loads-Apply-Stuctural-Forse/Moment
Давление (PRES)	Поверхностные нагрузки	SF	Main Menu>Solutions>-Loads-Apply-Stuctural-Pressure
Температура (TEMP) Обтекание (FLUE)	Объемные нагрузки	BF	Main Menu>Solutions>-Loads-Apply-Stuctural-Temperature
Гравитация, вращение	Инерционные нагрузки	-	Main Menu>Solutions>-Loads-Apply-Stuctural-Other

Приложение нагрузок с использованием команд
В таблице 6.3 приведены команды приложения нагрузок для динамического анализа переходных процессов.
Таблица 6.3

Тип нагрузки	Тведотельная или конечно-элементная модель	Объекты	Приложение	Удаление	Печать	Операции	Опции
1	2	3	4	5	6	7	8
Перемещения	Твердотельная	Точки	DK	DKDELE	DKLIST	DTRAN	-
Твердотельная	Линии	DL	DLDELE	DLLIST	DTRAN	-
Твердотельная	Поверхности	DA	DADELE	DALIST	DTRAN	-
Конечно-элементная	Узлы	D	DDELE	DLIST	DSCALE	DSYM DSUM
Силы	Твердотельная	Точки	FK	FKDELE	FKLIST	FTRAN	-
Конечно-элементная	Узлы	F	FDELE	FLIST	FSCALE	FSUM
Давление	Твердотельная	Линии	SFL	SFLDELE	SFLLIST	SFTRAN	SFGRAD
Твердотельная	Поверхности	SFA	SFADELE	SFALIST	SFTRAN	SFGRAD
Конечно-элементная	Узлы	SF	SFDELE	SFLIST	SFSCALE	SFGRAD SFCUM
Конечно-элементная	Элементы	SFE	SFEDELE	SFELIST	SFSCALE	SFGRAD SFBEAM SFFUN SFCUM

Продолжение табл.6.3

1	2	3	4	5	6	7	8
Температура, Обтекание	Твердотельная	Точки	BFK	BFKDELE	BFKLIST	BFTRAN	-
Твердотельная	Линии	BFL	BFLDELE	BFLLIST	BFTRAN	-
Твердотельная	Поверхности	BFA	BFADELE	BFALIST	BFTRAN	-
Твердотельная	Объемы	BFV	BFVDELE	BFVLIST	BFTRAN	-
Конечно-элементная	Узлы	BF	BFDELE	BFLIST	BFSCALE	BFSUM
Конечно-элементная	Элементы	BFE	BFEDELE	BFELIST	BFSCALE	BFSUM
Инерционные	-	-	ACEL OMEGA DOMEGA CGLOC CGOMGA DCGOM IRLF	-	-	-	-

Приложение нагрузки с использованием интерфейса.
Приложение нагрузок на линии.
Main Menu>Solutions>-Loads-Apply-Stuctural-Displasiment>On Lines
Печать нагрузок
Utility Menu>List>Loads>Load type
Возможные опции шагов нагрузки для динамического анализа переходных процессов приведены в таблице 6.4.
Таблица 6.4

Опция	Команда	Действия в интерфейсе
Динамические опции
Эффект интегрирования по времени	TIMINT	Main Menu>Solutions>-Loads Step Opt-Time/Frequense > Time Integration
Переходные параметры интегрирования	TINTP	Main Menu>Solutions>-Loads Step Opt-Time/Frequense > Time Integration
Демпфирование	ALPHAD BETAD MP,DAMP	Main Menu>Solutions>-Loads Step Opt-Time/Frequens > Damping
Основные опции
Время	TIME	Main Menu>Solutions>-Loads Step Opt-Time/Frequens > Time & Time Step или Time & Substep
Скачкообразная или плавно изменяющаяся нагрузка	KBC	Main Menu>Solutions>-Loads Step Opt-Time/Frequens > Time & Time Step или Time & Substep

Продолжение табл. 6.4

Шаг интегрирования по времени	NSUBST DELTIME	Main Menu>Solutions>-Loads Step Opt-Time/Frequens > Time & Substep или Time & Time Step
Автоматический выбор шага	AUTOTS	Main Menu>Solutions>-Loads Step Opt-Time/Frequens > Time & Substep или Time & Time Step
Опции учета нелинейностей
Максимальное число итераций	NE QIT	Main Menu>Solutions>-Loads Step Opt- Nonlinears > Equlibrium Iter
Допуск сходимости	CNVTOL	Main Menu>Solutions>-Loads Step Opt- Nonlinears > Convergence Crit
Опция коррекции предсказания	PRED	Main Menu>Solutions>-Loads Step Opt- Nonlinears > Predictor
Опции исследования линий	LNSRCH	Main Menu>Solutions>-Loads Step Opt- Nonlinears > Line Search
Критерий «ползучести»	CRPLIM	Main Menu>Solutions>-Loads Step Opt- Nonlinears > Creep Criterion
Опции окончания решения	NCNV	Main Menu>Solutions>-Loads Step Opt- Nonlinears > Criteria To Stop
Опции управления выходом
Выход на принтер	OUTPR	Main Menu>Solutions>-Loads Step Opt- Output Ctrls > Solu Printout
База данных и результирующий файл	OUTRES	Main Menu>Solutions>-Loads Step Opt- Output Ctrls > DB/Results File
Экстраполяция результатов	ERSX	Main Menu>Solutions>-Loads Step Opt- Output Ctrls > Integration Pt

3.1 Динамические опции включают следующее:

Эффект интегрирования по времени [TIMINT]

Эффект интегрирования по времени может быть включен для учета инерции и эффекта демпфирования (при выключенном состоянии получаем статическое решение). По умолчанию эффект интегрирования по времени включен. Эта опция полезна для начала перехода от начального статического решения. Первый шаг выполняется с выключенной опцией эффекта интегрирования по времени.

Переходные параметры интегрирования [TINTP]

Переходные параметры интегрирования управляют работой программы интегрирования по Ньюмарку. По умолчанию используется метод среднего ускорения. См раздел по основам теории.

Демпфирование

Демпфирование в некоторой форме присутствует в большинстве систем и должно быть учтено при решении задачи. Вы можете выбрать четыре формы демпфирования в полном динамическом анализе:

Alpha (демпфирование, пропорциональное массе) [ALPHAD];
Beta (демпфирование, пропорциональное жесткости) [BETAD];
Демпфирование, зависящее от свойств материалов [MP, DAMP];
Демпфирование элементов (Например, элемент COMBIN7).

6.5 Основные опции.
Основные опции включают следующее:

Время [TIME]

Эта опция определяет время в конце шага нагрузки.

Скачкообразная или плавно изменяющаяся нагрузка [KBS].

Эта опция показывает, изменяется ли нагрузка плавно за шаг [KBC] или скачкообразно [KBC,1]. По умолчанию принято плавное изменение нагрузки для статического анализа и скачкообразное для полного динамического анализа, когда опция SOLCONTROL включена.

Шаг интегрирования по времени [DELTIM или NSUBST].

Шаг интегрирования по времени является приращением времени при интегрировании уравнений движения. Вы можете его непосредственно [DELTIM], или определить по числу подшагов [NSUBST]. Размер временного шага определяет точность решения: чем меньше размер шага, тем выше точность. Рекомендации по выбору размера временного шага приведены позднее.

Автоматический выбор шага [AUTOTS].

Эта опция, известная как оптимизация временного шага в переходном анализе, увеличивает или уменьшает размер шага в зависимости от реакции системы. Для большинства задач мы рекомендуем включить автоматический выбор с верхним и нижним пределами размеров шага. Эти пределы выбираются с использованием команд DELTIM или NSUBST. По умолчанию эта опция включена, когда включена опция SOLCONTROL.
6.6 Опции учета нелинейностей.
Опции учета нелинейностей используются, только если в системе присутствуют нелинейности (пластичность, контактные элементы, ползучесть и т.д.). Они включают следующее:

Максимальное число итераций [NEQIT];
Точность сходимости [CNVTOL];
Опция коррекции предсказания [PRED];
Опция исследования линии [LNSRCH];
Критерий ползучести [CRPLIM];
Опция окончания решения [NCNV].

Более подробную информацию о применении этих опций см. «Руководство по нелинейным задачам».
6.7. Опции управления выходом.
Опции управления выходом включают следующее:

Выход на принтер [OUTPR]

Использование этой опции позволяет включить некоторые результаты в выходной файл (Jobname.OUT).

База данных и результирующий выходной файл [OUTRES]

Эта опция позволяет контролировать данные в результирующем файле (Jobname.RST)

Экстраполяция результатов [ERESX].

Применение этой опции позволяет просматривать результаты интегрирования точки элемента копированием их на узлы вместо их экстраполяции. (По умолчанию).
Внимание: По умолчанию только последний шаг по времени записывается в результирующий файл при полном методе динамического анализа. Для записи всех шагов установите поле FREQ команды OUTRES в положение «ALL». Максимум 1000 шагов записываются в результирующий файл по умолчанию. Для увеличения ресурсов памяти используйте команду /CONFIG,NRES.
Иногда правильное использование команд OUTRES или OUTPR может приводить к некоторым затруднениям.

Пример файла нагрузки приведен ниже.
TIME,….. | Время окончания первого шага нагрузки
LOADS . ..| Значение нагрузки при времени свыше
KBC,         | Плавная или скачкообразная нагрузка
LSWRITE | Запись данных в файл шага нагрузки
TIME, … . | Время конца второго шага нагрузки
LOADS… | Значение нагрузки при времени свыше
KBC,…     | Плавная или скачкообразная нагрузка
LSWRITE | Запись данных в файл шага нагрузки
TIME,….. | Время окончания третьего шага нагрузки
LOADS ... |Значение нагрузки при времени свыше
KBC          | Плавная или скачкообразная нагрузка
LSWRITE | Запись данных в файл шага нагрузки
И т. д
4. Сохраните конфигурацию нагрузки каждого шага нагрузки через интерфейс или командой LSWRITE:
Main Menu>Solution>Write LS File.
Повторите шаги 3, 4 для каждого угла кривой время-нагрузка. Вы можете захотеть иметь дополнительный шаг нагрузки, расширяющий последнюю точку по времени на кривой, для учета реакции системы после действия нагрузки.
5.     Сохраните копию базы данных в файл задачи. Вы можете затем перезагрузить ANSYS и воспользоваться командой RESUME.
Utility Menu>File>Save As
6.     Запустите задачу на решение. Дополнительные возможности построения и решения задач с многочисленными шагами нагрузок (метод массива параметров) приведены в разделе 3.10 руководства по процедурам ANSYS.
Команда LSSOLVE.
Интерфейс: Main Menu>Solution>Solve-From Ls Files
7.     Закройте меню SOLUTION.
6.8 Просмотр результатов
Результаты динамического анализа переходных процессов записаны в результирующем файле Jobname.RST. Они состоят из следующих данных, которые являются функциями времени:

Прямые данные;
Узловые перемещения (UX,UY,UZ,ROTX,ROTY,ROTZ).
Производные данные:
Напряжения в узлах и элементах;
Деформации в узлах и элементах;
Силы в элементах;
Усилия реакций в узлах;
И т.д.

Вы можете просмотреть эти результаты, используя постпроцессор POST26 или POST1:

POST26 используется для просмотра результатов специфических точек модели как функции времени;
POST1 используется для просмотра результатов полной модели в некоторый момент времени.

Некоторые типичные операции постпроцессора для анализа переходных процессов приведены ниже.

Необходимо помнить:

Для просмотра результатов в POST26 или POST1 база данных должна содержать ту же самую модель, для которой получено решение;
Должен быть получен файл Jobname.RST.

6.8.1 Использование POST26.
POST26 работает с таблицей результатов в функции времени, известных как переменные. Каждая переменная имеет свой ссылочный номер. Переменная с номером 1 зарезервирована для времени.
Команды определения переменных:
NSOL (Прямые данные, перемещения узлов);
ESOL(Производные данные, Решения элементов, например, напряжения);
RFORCE (Силы реакции);
FORCE(Полные силы, статическая, демпфирующая, или инерционная составляющая);
SOLU (размер временных шагов, максимальное число итераций, частота реакции и т. д.).
Интерфейс:
Main Menu>TimeHist Postpro>Define Variables
Примечание: В редуцированном методе и методе суперпозиций мод учитываются только статические силы в команде FORCE.
Рисование или распечатка переменных. Просматривая результаты в функции времени, вы можете выбрать критические моменты времени для дальнейшего использования постпроцессора POST1.
Команды:
PLVAR (графические переменные);
PRVAR, EXTREM (Печать переменных).
Интерфейс:
Main Menu>TimeHist Postpro>Graph Variables
Main Menu>TimeHist Postpro>List Variables
Main Menu>TimeHist Postpro>List Extreme
В POST26 имеется множество функций, таких как математические операции, перемещение переменных в массив параметров, перемещение массива параметров в переменные.
6.8.2 Использование POST1.
1. Чтение данных из базы данных:
Команда: RESUME.
Интерфейс: Utility Menu>Resume from.
Прочесть желаемый набор результатов. Используйте команду SET для идентификации данных по номеру временных шагов или по времени.
Команда SET.
Интерфейс:
Main Menu>General Postpro>Read Result-By Time/Freq
Примечание: Если вы определили время, для которого нет результатов, результат будет получен линейной интерполяцией между двумя ближайшими точками по времени.

Опция деформированное состояние
Команда PLDISP .
Интерфейс: Main Menu> General Postproc > Plot Results > Deformed Shape
Опция печати усилий реакций и моментов
Команда PRRSOL.
Интерфейс: Main Menu> General Postproc > List Results > Reaction Solu.
Примечание: Команда PRRSOL распечатывает силы и моменты в закрепленных узлах. Для показа сил реакции введите: /PBS,RFOR,,1 , затем для показа требуемого узла или элемента [NPLOT или EPLOT]. Используйте команду RMOM вместо RFOR для реакции моментов.
Опция печати узловых сил и моментов
Команда PRESOL,F (или M).
Интерфейс: Main Menu> General Postproc > List Results > Element Solution.
Вы можете распечатать сумму узловых сил и моментов для выбранного набора узлов.
Команда FSUM.
Интерфейс: Main Menu> General Postproc > Nodal Calcs > Total Force Sum.
Вы можете проверить суммарные силы и суммарные моменты в каждом выбранном узле. Из условия равновесия, суммарные силы должны быть равны нулю, исключая точки приложения внешних сил и узлы, где возникают реакции.
Команда NFORCE .
Интерфейс: Main Menu> General Postproc > Nodal Calcs>Sum @ Each Node.
Команда FORCE (Main Menu> General Postproc > Options for Outp) требует указать какой именно компонент необходимо вывести:

Полные (по умолчанию);
Статические;
Демпфирующие;
Инерциальные.

Из условия равновесия, суммарные силы должны быть равны нулю, исключая точки приложения внешних сил и узлы, где возникают реакции.
Опция результаты элементов на линии (построение эпюр).
Команда ETABLE
Интерфейс:
Main Menu> General Postproc > Element Table > Define Table.
Для элементов, расположенных на линиях, таких как балки, стержни, трубы использование этой опции увеличивает наглядность производных данных (напряжения, деформации и т. д.). Результирующие данные идентифицируются с помощью комбинаций меток и ссылочных номеров, или наименований компонентов в команде ETABLE. (См. раздел построения таблиц элементов).
Опция печати ошибок приближения.

Команда PRERR.
Интерфейс: Main Menu> General Postproc > List Results > Persent Error.
Для линейного статического анализа с использованием объемных или оболочечных элементов применение команды PRERR позволяет оценить ошибку решения по отношению к степени разбиения. Эта команда рассчитывает процент ошибки нормы энергии системы (SEPC), которая представляет относительную ошибку дискретизации при разбиении.
Опция рисования контуров ошибок приближения.
Команда PRESOL,SERR
Интерфейс: Main Menu> General Postproc > Plot Results > Contour Plot-Element Solu
Использование команды PRESOL,SERR позволяет рисовать ошибки в энергии системы от элемента к элементу. Регионы модели с высокой нормой ошибки энергии – хорошие кандидаты для пересмотра уровня разбиений.
Опция рисования контуров.
Команда: PRNSOL или PRESOL .
Интерфейс: Main Menu> General Postproc > Plot Results > Contour Plot-Nodal Solu или Element Solu.
Использование этой опции позволяет рисовать такие результаты, как напряжения (SX, SY, SZ…), деформации (EPELX, EPELY, EPELZ…) и перемещения (UX, UY, YZ…).
Вы можете изобразить контуры данных таблицы элементов (эпюры) для элементов, расположенных на линиях.
Команда: PLETAB,PLLS
Интерфейс: Main Menu> General Postproc > Element Table > Plot Element Table
Main Menu> General Postproc > Plot Results > Contour Plot-Line Elem Res
Примечание: Производные данные, такие как напряжения и деформации усредняются в узлах при использовании команды PLNSOL. Этот результат “загрязняется” в улах, имеющих различные материалы в элементах, различные толщины в оболочках или при других особенностях. Для того, чтобы избежать этих ошибок, перед рисованием выбирайте элементы имеющие одинаковый материал, одинаковую толщину оболочки и т.д. Или используйте Power Graphic с командой AVRES (Main Menu> General Postproc > Options for Outp) для выключения режима усреднения.
Опция векторного рисования.
Команда PLVEC (рисование векторов), PRVEC (печать векторов).

Интерфейс:
Main Menu> General Postproc > Plot Results > Vector Plot-Predefined
Main Menu> General Postproc > List Results > Vector Data.
Векторы показывают (не путайте с векторными модами) эффективные траектории векторных величин, таких, как перемещения, вращения и напряжения.
Опция табулированной печати.
Команды:
PRNSOL (результат решения в узлах);
PRESOL (Результат от элемента к элементу)
PRRSOL (Реакции)
NSORT, ESORT
Интерфейс:
Main Menu> General Postproc > List Results >solution option
Main Menu> General Postproc > List Results >Sorted Listing-Sort Nodes или Sort Elems.
В POST1 предусмотрено много других функций: масштабирование результатов, комбинация случаев нагружения и т.д.
Ниже приведен пример ввода задачи командным методом.
Построение модели
/FILNAM,….                 | Имя задачи
/TITLE,….                      |Титул
/PREP7                             |Вход в препроцессор
--------
--------                           | Построение модели
FINISH
Приложение нагрузок и получение решения
/SOLU                         |Режим решения
ANTYPE,TRANS       |Анализ переходных процессов
TRNOPT,FULL           |Полный метод
D,                                 |Закрепления
F,                                  |Силы
SF,
ALPHAD,                     |Демпфирование, пропорциональное массам
BETAD,                        | Демпфирование, пропорциональное жесткости
KBC,                             | Плавная или скачкообразная нагрузка
TIME,                            |Время конца шага нагрузки
AUTOTS,ON                |Автоматический выбор временного шага
DELTIM,                       |Размер временного шага
OUTRES,                       |Опции результирующего файла
LSWRITE                       |Запись первого шага нагрузки
-----------
----------
----------                            |Нагрузки, время и т.д. для второго шага нагрузки
LSWRITE                        |Запись второго шага нагрузки

SAVE
LSSOLVE,1,2                  |Инициализация решения с несколькими шагами нагрузки
FINISH
Просмотр результатов
/POST26
SOLU,
NSOL,                                | Накопление результатов по узлам как переменных
ESOL,,,,                             | Накопление результатов по элементам как переменных
RFORCE                            |Накопление реакций как переменных
PLVAR,                             |Рисование графиков
PRVAR                              |Печать переменных
FINISH
/POST1
SET,                                   |Чтение результатов в базу данных
PLDISP,                             |Деформированное состояние
PRRSOL,                           |Усилия реакций
PLNSOL,                           |Рисование узловых результатов
PRERR,                             |Оценка процента ошибки
………
FINISH
6.9 Редуцированный динамический анализ переходных процессов
Редуцированный метод, как следует из его названия, использует редуцированные матрицы для расчета динамической реакции. Он возможен в программах ANSYS/Multiphysics, ANSYS/Mechanical, ANSYS/Structural. Вы должны рассмотреть применение этого метода, если вы не будете включать нелинейности (не более, чем контакт узла с узлом) в задачу.
Процедура редуцированного динамического анализа состоит из пяти основных шагов:
1.     Построение модели;
2.     Получение редуцированного решения;
3.     Просмотр результатов редуцированного решения;
4.     Расширение решения;
5.     Просмотр результатов расширенного решения.
Первый шаг тот же самый, что и для полного метода, исключая то, что не учитываются нелинейности (может быть учтен единственный контакт между двумя узлами, определяемый в форме условий зазора, вместо введения соответствующего элемента). Последующие шаги подробно рассмотрены ниже.
Редуцированное решение получается относительно главных степеней свободы. Порядок получения решения следующий:

1.     Войдите в режим решения с помощью команды /SOLU или через интерфейс:
Main Menu > Solution.
2.     Определите тип анализа и его опции. Это то же самое, что и для полного метода, за исключением следующих различий:

Выберите редуцированный метод решения [TRNOPT];
Опции учета нелинейностей не возможны [NLGEOM, SSTIF, NROPT];
Вы можете включить эффекты предварительного напряжения [PSTRES]. Это требует файла элементов из предшествующего статического или переходного анализа;
Рестарт невозможен [ANTYPE].

3. Определите главные степени свободы. Они должны в основном характеризовать динамическое поведение системы. Для редуцированного анализа переходных процессов, главные степени свободы необходимо выбирать там, где вы хотите определить условия зазора, приложить силы или не нулевые перемещения. Вы можете распечатать выбранные главные степени свободы, или уничтожить их.
Команды:
M
MGEN
TOTAL
MLIST
MDELE
Действия в интерфейсе:
Main Menu>Solution>Master DOFs>Define/Copy/Program Selected
Main Menu>Solution>Master DOFs>List All
Main Menu>Solution>Master DOFs>Delete.
4. Определите условия зазора, если это необходимо.
Команда GP
Main Menu>Solution>Dynamic Gap Cond>Define
Вы можете распечатать условия или удалить их
Команды:
GPLIST
GPDELE
Main Menu>Solution>Dynamic Gap Cond>List All
Main Menu>Solution>Dynamic Gap Cond>Delete
Условия зазора
Условия зазора могут быть определены только между двумя главными узлами или между главными узлами и опорой, как показано на рисунке.

Условия зазора похожи на элемент типа зазора и выбирается между поверхностями, между которыми предполагается контакт (удар) в процессе переходного процесса. ANSYS учитывает усилия в зазоре, которые развиваются, когда зазор закрыт с использованием эквивалентного узлового вектора нагрузок. Некоторые рекомендации по определению условий зазора приведены ниже.

Используйте достаточные условия для получения равномерного распределения контактного напряжения между контактирующими поверхностями.
Определите обоснованную контактную жесткость. Если жесткость слишком мала, контактирующие поверхности перекроются слишком много. Если жесткость слишком высока, очень малый временной шаг будет требоваться для времени удара. Основными рекомендациями является выбор жесткости зазора на один или два порядка выше, чем жесткость соседних элементов. Вы можете определить жесткость соседних элементов, используя соотношение AE/L, где A- эффективная площадь контакта, E- модуль упругости наиболее мягкого материала в зазоре, L – глубина первого слоя элементов в зазоре.

5. Введите начальные условия для модели. Следующие нагрузки возможны в редуцированном анализе переходных процессов:

Возможны только перемещения, силы, и поступательные ускорения (такие, как гравитация). Нагрузки от ускорения не поддерживаются, если модель содержит некоторые главные координаты в узлах с вращением узловых координатных систем.
Силы и ненулевые перемещения должны быть приложены только к главным степеням свободы.

Как указывалось для полного метода, многочисленные шаги нагрузки обычно требуют определения «истории нагрузки» в переходном анализе. Первый шаг используется для установления начальных условий. Второй и последующие шаги нагрузки используются для ввода значений.

Установите начальные условия. Начальные условия могут быть установлены в явном виде только для перемещений (
), начальные скорости и ускорения должны быть равны нулю.
. Перемещения не могут быть уничтожены в последующих шагах нагрузки, тем не менее, они не могут быть использованы для определения начальной скорости. В редуцированном переходном анализе статическое решение всегда рассматривается как предварительное решение, используемое для определения
.
Определите опции шагов нагрузки для первого шага. Возможны следующие опции для первого шага (см. табл. 6.5).

Таблица 6.5
Опции для первого шага нагрузки

Опция	Команда	Действия в интерфейсе
Динамические опции
Параметры интегрирования	TINTP	Main Menu>Solutions>-Loads Step Opt-Time/Frequens > Time Integraton
Демпфирование	ALPHAD BETAD MP,DAMP	Main Menu>Solutions>-Loads Step Opt-Time/Frequens > Damping
Основные опции
Шаг интегрирования по времени	DELTIM	Main Menu>Solutions>-Loads Step Opt-Time/Frequens > Time & Time step
Опции управления выводом
Вывод на печать	OUTPR	Main Menu>Solutions>- Loads Step Opt- Output Ctrls > Solu Printout

Динамические опции.
Динамические опции включают следующее:

Параметры интегрирования [TINTP].

Этот параметр управляет процессом интегрирования по алгоритму Нъюмарка. По умолчанию используется метод среднего ускорения.

Демпфирование.

Демпфирование в некоторой форме присутствует в большинстве систем и должно быть учтено при решении задачи. Вы можете выбрать четыре формы демпфирования в редуцированном динамическом анализе:

Alpha (демпфирование, пропорциональное массе) [ALPHAD];
Beta (демпфирование, пропорциональное жесткости) [BETAD];
Демпфирование, зависящее от свойств материалов [MP, DAMP];
Демпфирование элементов (например, элемент COMBIN7).

Основные опции

Шаг интегрирования [DELTIM]

Шаг интегрирования принимается постоянным.
Если вы введете команду TIME для первого шага нагрузки, она будет игнорироваться. Первое решение всегда статическое при T=0.
Опции управления выводом.
Опции управления выводом включают следующее:

Вывод на принтер [OUTPR].

Использование этой опции выводит перемещения на главных степенях свободы.
6. Запишите первый шаг нагрузки в файл (Jobname.S01).
Команда: LSWRITE.
Интерфейс: Main Menu>Solutions>-Solve-Write Ls File
7. Задайте нагрузки и опции шагов нагрузки для анализа переходных процессов, записывая каждый шаг нагрузки в файл [LSWRITE].

Следующие шагов нагрузки поддерживаются для анализа переходных процессов:
Основные опции

Время (Time) (Определяется время конца каждого шага нагрузки).
Скачкообразная [KBC,1] или плавная нагрузка [KBC].

Управление выводом

Выход на принтер [OUTPR].
Редуцированный файл перемещений [OUTRES].

Перед определением переменных в POST 26 используйте команду FILE (Main Menu>TimeHist Postpro>Setting>File) для выбора данных для чтения данных из файла Jobname.RDSP. Например, если наименование задачи – TRANS, то полная команда FILE будет FILE,TRANS,RDSP.
Только данные степеней свободы узлов (главных степеней свободы) возможны для просмотра.

6.9.2 Расширение решения.
Расширенное решение запускается после редуцированного решения и рассчитывает полные перемещения, напряжения и силы по всем степеням свободы. Это решение будет получено только для одной точки по времени, которое вы выберите. Перед запуском расширенного решения вы должны просмотреть результаты редуцированного решения, используя POST26 и выбрать критическую точку по времени.

Примечание. Получение расширенного решения требуется не всегда. Например, если вас в основном интересуют перемещения в некоторых точках вашей конструкции, то редуцированное решение может вас удовлетворить. Безусловно, если вы хотите определить перемещения в не главных степенях свободы, или вас интересуют напряжения и силы, вы должны получить расширенное решение.

Файлы с расширениями .RDSP, .EMAT, .ESAV, .DB и .TRI должны быть получены в редуцированном решении.
База данных должна содержать ту же самую модель, для которой получено редуцированное решение.

1. Перезапустите решение.
Команда /SOLU
Main Menu>Solution
2. Активизируйте решение расширения и его опции.

Опции	Команда	Действия в интерфейсе
Решение расширения вкл/выкл	EXPASS	Main Menu>Solution>-Analis Type-Expansion Pass
Номера расширяемых решений	NUMEXP	Main Menu>Solution>Load Step Opts-Expansion Pass>Range Of Solus
Расширение единственного решения	EXPSOL	Main Menu>Solution>Load Step Opts-Expansion Pass>Single Expand-By Time/Freq

Опция Решение расширения вкл/выкл. Выберите «ON».
Опция Номера расширяемых решений. Выберите номера. Эти решения будут расширятся в выбранном значении времени. Близь лежащие решения около этого времени будут расширяться. При этом нужно определить, нужно ли считать напряжения и силы (по умолчанию считается и то и другое).
Опция Расширение единственного решения. Используйте эту опцию для идентификации единственного решения для расширения, если нет необходимости расширять несколько решений. Вы можете выбрать его по шагу нагрузки и номеру временного шага или по времени.
3. Выберите опции шагов нагрузки. Подходящие опции управления выходом для расширения динамического анализа.

Опция выхода на принтер [OUTPR]

Используйте эту опцию для включения некоторых результатов в выходной файл (Jobname.OUT).

База данных и результирующий файл [OUTRES]

Эта опция контролирует данные в результирующем файле (Jobname.RST).

Экстраполяция результатов [ERESX]

Использование этой опции используется для просмотра результатов точек интегрирования элементов копированием их на узлы вместо экстраполяции их (по умолчанию).
Примечание: поля FREQ в командах OUTPR и OUTRES могут быть ALL или NONE.
4.     Запустите решение расширения.
Команда SOLVE.
Интерфейс
Main Menu>Solution>-Solve-Current LS.
5.     Повторите шаги 2, 3 и 4 для дополнительных решений расширения. Каждый шаг расширения сохраняется как отдельный шаг нагрузки в результирующем файле.
6.     Выйдите из режима решения.
Результаты расширенного решения записываются в результирующий файл Jobname.RST. Они состоят из следующих данных, рассчитанных для каждой временной точки, для которой получено редуцированное решение.

Прямые данные;
Узловые перемещения (UX,UY,UZ,ROTX,ROTY,ROTZ).
Производные данные:
Напряжения в узлах и элементах;
Деформации в узлах и элементах;
Силы в элементах;
Усилия реакций в узлах;
И т.д.

Вы можете просмотреть эти результаты, используя POST1. Если вы получили расширенное решение для нескольких временных точек, вы можете использовать POST26 для получения графика напряжений, деформаций или сил в функции времени. Процедура использования POST1 или POST26 та же самая, как и для полного метода.
6.10 Пример анализа переходных процессов.
В этом примере рассмотрен анализ переходного процесса с использованием редуцированного метода при постоянной силе с конечным временем ее нарастания. В этой задаче стальная балка с сосредоточенной массой подвергается воздействию динамической нагрузки.
Стальная балка длиной l поддерживает сосредоточенную массу m. На балку действует динамическая нагрузка F(t) c временем возрастания

и максимальным значением

. Если вес балки не учитывается, определить время, при котором будет максимальное перемещение

и величину максимального перемещения

. Еще нужно определить максимальное напряжение в балке.
Балка не использовалась в этом решении, и ее площадь принималась как единица.

Полное время 0, 1с позволяет массе достигнуть максимальных перемещений. Главная степень свободы принималась на массе в поперечном направлении. Статическое решение получено на первом шаге нагрузки. Время максимальной реакции (0,092с) было выбрано для расширения решения.
Условия задачи
E=30*103 ksi,

kips sec2/in, J=800.6 in4

=18 in, l=240 in (20ft), F1=20 kips

=0,075с.
Рис. 6.3 Расчетная схема балки
Определение титула задачи.
1.     Utility Menu>File>Change Title
2.     Введите текст «Transient response to a constant force with a finite rise time»
3.     Нажмите ОК.
Определение типа элементов
1.     Main Menu>Prepocessor>Element Type>Add/Edit/Delete
Откроется диалоговый «ящик»
2.     Нажмите на Add. Откроется диалоговый «ящик» библиотеки элементов.
3.     В левой части нажмите на «Structural Beam»
4.     В правой части нажмите на «2D elastic 3” и нажмите на Apply
5.     В левой части нажмите на «Structural mass»
6.     В правой части нажмите на «3D mass 21» и нажмите «ОК»
7.     В диалоговом «ящике» нажмите один раз на «Type2» и нажмите на «Options».
8.     В диалоговом окне для опции инерции при вращении найти «2Dw/o rot iner» и выбрать ее.
9.     Нажать «ОК» и на «Close» в диалоговом ящике типа элементов.
Определение реальных констант.
1.     Main Menu>Preprocessor>Real Constants
2.     Нажать на Add. Откроется диалоговое окно типов элементов для реальных констант.
3.     Нажать ОК. Откроется диалоговое окно для BEAM3
4.     Введите 1 для площади, 800,6 для IZZ и 18 для высоты балки.
5.     Нажать на ОК.
6.     На диалоговом окне реальных констант нажать на «Add»

7.     Нажать на тип 2 MASS21 и нажать на ОК. Диалоговое окно для реальных констант для MASS21 откроется.
8.     Введите 0.0259087 для 2D массы и нажать на ОК.
9.     Нажать на Close диалогового окна реальных констант.
Определение свойств материалов.
1.     Main Menu>Preprocessor>Material Props>-Constant –isotropic откроется диалоговое окно свойств материалов.
2.     Нажать ОК. Откроется второе диалоговое окно.
3.     Ввести 30e3 для модуля упругости EX и нажать ОК.
Определение узлов
1.        Main Menu > Preprocessor > Modeling-Create > Nodes > in Active CS Откроется диалоговое окно построения узлов в активной системе координат.
2.        Введите 1 для номера узла и нажмите «Apply» для определения узла с координатами 0,0,0.
3.        Введите 3 для номера узла.
4.        Введите 240,0,0 для координат и нажмите ОК.
5.        Построение узлов между двумя заданными. Main Menu > Preprocessor > Modeling-Create > Nodes > Fill between Nds. Откроется соответствующее меню.
6.        Нажать один раз на узлы 1 и 3 и нажать на ОК.
7.        Нажать ОК, приняв установки по умолчанию.
Определение элементов
1.     Main Menu > Preprocessor > Modeling-Create > Elements > Auto Numbered> Thru Nodes.
2.     Нажать на узлы 1 и 2 и нажать на Apply
3.     Нажать на узлы 2 и 3 и нажать ОК.
4.     Main Menu > Preprocessor > Modeling-Create > Elements > Elem Attributes. Откроется диалоговое окно атрибутов элементов.
5.     Выбрать 2 для элементов типа MASS21

6.     Выбрать 2 для набора констант и нажать ОК.
7.     Main Menu > Preprocessor > Modeling-Create > Elements > Auto Numbered> Thru Nodes. Откроется пиковое меню элементов.
8.     Нажать один раз на узел 2 и нажать ОК.
Определение типа анализа и опций анализа.
1.     Main Menu > Solution> Analysis Type- New Analys
2.     Нажать на «Transient» и нажать на ОК.
3.     Main Menu > Solution> Analisis Option. Откроется диалоговое окно анализа переходных процессов.
4.     Нажать на «Reduced» и нажать ОК. Откроется диалоговое окно редуцированного анализа.
5.     В падающем меню для эффектов демпфирования выбрать «Ignore».
6.     Нажать ОК.
Определение главных степеней свободы
1.     Main Menu > Solution> Master DOFs >User Selected-Define. Откроется «пиковое» меню.
2.     Нажать на узел 2 и нажать ОК. Откроется диалоговое меню.
3.     В падающем меню для первой степени свободы выбрать «UY»
4.     Нажать ОК.
Установка опций шагов нагрузки.
1.     Main Menu > Solution> Load Step Opts-Time/Frequenc>Time – Time Step. Откроется диалоговое окно.
2.     Ведите 0.004 в качестве размера временного шага и нажать ОК.
Приложение нагрузки на первом шаге нагрузки
1.     Закрепление балки в узлах 1и 3. Main Menu > Solution> Loads Apply>-Structural-Displacement>On Nodes. Откроется «пиковое» меню.
2.     Нажать на узел 1 и нажать «Apply». Откроется диалоговое окно.
3.     Выбрать «UY» и нажать на «Apply».
4.     Нажать на узел 3 и нажать ОК. Откроется диалоговое окно.
5.     Нажать на «UX», «UY» будет уже выбрано. Нажать ОК.

6.     Приложение нагрузки. Main Menu > Solution> Loads Apply>-Structural-Force/Moment>On Nodes. Откроется пиковое меню.
7.     Нажать на узел 2 и нажать ОК. Откроется диалоговое окно.
8.     В падающем меню для направления сил выбрать «FY», ввести значение 0 для начального статического решения.
9.     Нажать на ОК и нажать SAVE_DB
Установка опций вывода.
1.     Main Menu > Solution> Load Step Opts>-Output Ctrls>DB/Results File. Откроется диалоговое окно.
2.     Нажмите на кнопку «Every substep» (Каждый шаг) и нажмите ОК.
Решение первого шага нагрузки.
1.     Main Menu>Solution>-Solve-Current LS.
2.     Просмотрите информацию в окне статуса и нажмите «Close».
3.     Нажмите ОК на диалоговом окне текущего шага нагрузки для начала решения.
4.     Нажмите на «Close», когда решение будет получено.
Приложение следующего шага нагрузки.
1.     Main Menu > Solution> Load Step Opts-Time/Frequenc>Time – Time Step. Откроется диалоговое окно опций времени и временных шагов.
2.     Ввести 0.075 для (Time) конца шага нагрузки нажать ОК.
3.     Main Menu > Solution> Loads Apply>-Structural-Force/Moment>On Nodes. Откроется пиковое меню.
4.     Нажать на узел 2 и нажать ОК. Откроется диалоговый «ящик».
5.     Ввести 20 как значение силы и нажать ОК.
Решение следующего шага нагрузки.
1.     Main Menu>Solution>-Solve-Current LS.
2.     Просмотрите информацию в окне статуса и нажмите «Close»
3.     Нажмите ОК на диалоговом окне текущего шага нагрузки для начала решения.
4.     Нажмите на «Close», когда решение будет получено.
Установка следующего шага нагрузки и решение.

1.     Main Menu > Solution> Load Step Opts-Time/Frequenc>Time – Time Step Откроется диалоговое окно опций времени и временных шагов.
2.     Введите 0.1 для (Time) конца шага нагрузки нажмите ОК.
3.     Main Menu>Solution>-Solve-Current LS.
4.     Просмотрите информацию в окне статуса и нажмите «Close»
5.     Нажмите ОК на диалоговом окне текущего шага нагрузки для начала решения.
6.     Нажмите на «Close», когда решение будет получено.
7.     Main Menu>Finish
Расширение решения
1.     Main Menu > Solution> Analysis Type- Expansion Pass. Включите кнопку «Expansion pass» в положение «ON» и нажмите ОК.
2.     Main Menu > Solution> Load Step Opts-Expansion Pass>Single Expand – By Time/Freq. Откроется диалоговое меню.
3.     Введите 0.092 для временной точки и нажмите ОК.
4.     Main Menu>Solution>-Solve-Current LS.
5.     Просмотрите информацию в окне статуса и нажмите «Close».
6.     Нажмите ОК на диалоговом окне текущего шага нагрузки для начала решения.
7.     Нажмите на «Close», когда решение будет получено.
Просмотр результатов в POST26.
1.     Main Menu>Time Hist Postpro>Setting>File. Откроется диалоговое меню.
2.     В меню выбрать “file.rdsp» и нажать ОК.
3.     Выбор переменных. Main Menu>Time Hist Postpro>Define Variables. Откроется диалоговое окно.
4.     Нажать на “Add» (Добавить). Откроется диалоговое окно переменных.
5.     Выбрать (по умолчанию) решение в узлах (Nodal DOF result) и нажать ОК. Откроется диалоговое меню данных узлов.
6.     Выбрать 2 (по умолчанию) как ссылочный номер переменной.

7.     Ввести 2 как номер узла.
8.     Ввести NSOL как метку пользователя.
9.     В правой части окна выбрать «Translation UY».
10.            Нажать ОК, затем «Close» на диалоговом окне переменных.
11.            Main Menu>Time Hist Postpro>Graph Variables.
12.            Введите 2 для первой переменной графика и нажмите ОК. Возникнет график в графическом окне.
13.            Main Menu>Time Hist Postpro>List Variables.
14.            Введите 2 для первой переменной и нажмите ОК.
15.            Просмотрите информацию и нажмите «Close».
Просмотр результатов в POST1.
1.     Main Menu>General Postproc>Read Results-First Set
2.     Main Menu>General Postproc>Plot Results-Deformed Shape
3.     Нажмите «Def+undeformed» и нажмите ОК.
Выход из ANSYS.
1.     Нажмите QUIT
2.     Нажмите на SAVE, если это необходимо
6.11 Метод суперпозиции мод в анализе переходных процессов.
Метод суперпозиции мод основан на суммировании коэффициентов формы мод, полученных из модального анализа, для расчета динамической реакции. Процедура использования метода состоит из пяти основных шагов:
1.     Построение модели;
2.     Получение модального решения (нахождение собственных частот и форм);
3.     Решение задачи переходного анализа методом суперпозиции мод;
4.     Расширение решения;
5.     Просмотр результатов.
Из перечисленных шагов первый -точно такой же, как и для полного метода.

6.11.1 Получение модального решения.
Вы должны иметь в виду следующие особенности:

Методы решения задачи могут быть следующие: редуцированный, блочный, подпространства, или Power Dynamic (два других метода несимметричный и демпфированный не применяются в методе суперпозиции мод). Вы можете использовать Power Dynamic, только если нет начальной статической нагрузки (все нагрузки равны нулю на первом шаге);
Необходимо раскрыть все моды, необходимые для переходного анализа;
Для редуцированного метода раскрытия мод, включите главные степени свободы тех узлов, в которых заданы силы и условия зазора.
Введите закрепления. Эти закрепления будут игнорироваться, если они определены в переходном анализе методом суперпозиции мод вместо модального анализа.
Если необходимо ввести нагрузки элементов (давление, температура, ускорения и т. д.) в переходном динамическом анализе, вы должны определить их модальном анализе. Нагрузки игнорируются в модальном анализе, но вектор нагрузки будет рассчитываться, и записываться в файл формы моды (Jobname.MODE). Вы можете затем использовать этот вектор нагрузки для переходного анализа.
Данные модели не должны изменяться между модальным и переходным анализом.
Нет необходимости раскрывать моды для метода суперпозиции мод. Если вы хотите просмотреть формы моды из редуцированного решения, вы должны раскрыть их.

6.11.2. Решение методом суперпозиции мод.
В этом шаге программа использует формы мод, полученных в модальном анализе. Необходимо помнить, что:

Файл формы мод должен быть получен (Jobname.MODE).
База данных должна содержать ту же самую модель, для которой получено решение модального анализа.

1. Введите команду /SOLU или через интерфейс: Main Menu>Solutions.
2. Определите тип анализа и его опции. Это то же самое, что описано для полного метода, исключая следующие особенности:

Выберите метод суперпозиции мод [TRNOPT].
Определите число мод для использования в решении [TRNOPT].

Это определяет точность переходного решения. Как минимум, вы должны использовать все моды, которые, по вашему мнению, влияют на динамическую реакцию системы. Например, если вы включаете в рассмотрение высокие частоты, то в число учитываемых мод должны быть включены высокочастотные моды. По умолчанию включаются все моды, полученные в модальном анализе.
Нелинейные опции [NLGEOM,SSTIF, NROPT] не учитываются.
Рестарт не возможен [ANTYPE].

3. Определите условия зазора, если это необходимо. Они могут быть определены только между двумя главными узлами или между главным узлом и «землей».
Команда GP . Интерфейс: Main Menu>Solutions>Dynamic Gap Cond>Define
4. Приложите нагрузки к модели. Возможны следующие нагрузки в методе суперпозиции мод:

Возможны только силы, поступательные ускорения и вектор нагрузок, сформированный в модальном анализе. Не нулевые перемещения игнорируются. Для приложения вектора нагрузки используется команда LVSCALE (Main Menu>Solutions>Loads - Apply>Load Vector>For Mode Super).
Если формы мод получены из редуцированного модального анализа, силы могут быть приложены только к главным степеням свободы.

Многочисленные шаги нагрузки обычно требуют определения «нагрузочной истории» в переходном анализе. Первый шаг нагрузки используется для определения начальных условий, а второй и последующие шаги используются для анализа переходных процессов.

Установите начальные условия. Начальные условия, которые можно точно задать это начальные перемещения. Статическое решение с использованием метода суперпозиции мод всегда рассматривается как первое решение при заданной нагрузке. Если для модального анализа использовалась программа POWER DYNAMICS, то ни нагрузки, ни перемещения не учитываются, то есть в этом случае принимаются только нулевые начальные условия.

Опции шагов нагрузки для первого шага

Опция	Команда	Действия в интерфейсе
Динамические опции
Параметры интегрирования	TINTP	Main Menu > Solution> Load Step Opts-Time/Frequenc>Time Integration
Вектор нагрузки	LVSCALE	Main Menu>Solutions>Loads - Apply>Load Vector>For Mode Super
Демпфирование	ALPHAD BETAD DMPRAT MP,DAMP	Main Menu>Solutions>-Loads Step Opt-Time/Frequens > Damping
Основные опции
Шаг интегрирования по времени	DELTIM	Main Menu>Solutions>-Loads Step Opt-Time/Frequens > Time & Time step
Опции управления выводом
Вывод на печать	OUTPR	Main Menu>Solutions>-Loads Step Opt- Output Ctrls > Solu Printout

Динамические опции
Динамические опции включают следующее:

Параметры интегрирования [TINTP].

Вектор нагрузки [LVSCALE]

Эта опция позволяет вам прикладывать вектор нагрузки, построенный в модальном анализе. Вы можете использовать такой вектор нагрузки для приложения нагрузок на элементы (давление, температура и т.д.)

Демпфирование.

Alpha (демпфирование, пропорциональное массе) [ALPHAD];
Beta (демпфирование, пропорциональное жесткости) [BETAD];
Постоянное отношение демпфирования [DMPRAT];
Демпфирование, зависящее от свойств материалов [MP, DAMP];
Модальное демпфирование [MDAMP];

Основные опции

Шаг интегрирования [DELTIM]

Шаг интегрирования принимается постоянным. По умолчанию шаг интегрирования принимается равным 1/(20f), где f низшая частота, учитываемая в решении. Команда [DELTIM] воспринимается только на первом шаге нагрузки, и игнорируется на последующих шагах.
Опции управления выводом.
Опции управления выводом включают следующее:

Вывод на принтер [OUTPR].

Использование этой опции выводит перемещения на главных степенях свободы.
5. Запишите первый шаг нагрузки в файл (Jobname.S01).
Команда: LSWRITE.
Интерфейс: Main Menu>Solutions>-Solve-Write Ls File
6. Задайте нагрузки и опции шагов нагрузки для анализа переходных процессов, записывая каждый шаг нагрузки в файл [LSWRITE].
Следующие шагов нагрузки поддерживаются для анализа переходных процессов:
Основные опции

Время (Time) (Определяется время конца каждого шага нагрузки).
Вектор нагрузки [LVSCALE]
Скачкообразная [KBC,1] или плавная нагрузка [KBC]. По умолчанию принимается плавная нагрузка.

Управление выводом

Выход на принтер [OUTPR].
База данных и результирующий файл [OUTRES].

Для всех этих команд правильной является метка NSOL (решение в узлах). По умолчанию для команды [OUTRES] записывается каждая четвертая точка по времени для редуцированного файла перемещений (если определены условия зазора, то записывается каждая точка решения).
7. Если использовался метод подпространства или блочный метод для модального анализа (MODOPT,SUBST или MODOPT,LANS) вы можете использовать компоненты узлов с помощью команды OUTRES,NSOL для ограничения данных перемещения, записываемый в редуцированный файл Jobname.RDSP. Решение с расширением будет давать правильные результаты только для этих узлов и для тех элементов, у которых все узлы записаны в файл Jobname.RDSP. Для использования этой опции сначала запретите запись командой OUTRES,NSOL,NONE, затем выберите объект OUTRES,NSOL,freq,cjmponent. Повторите команду для некоторых дополнительных компонентов узлов и запишите RDSP файл. Допустима только одна выходная частота. ANSYS использует последнюю частоту выбранную командой OUTRES.
8.     Сохраните копию база данных в файл с именем.
Команда SAVE.
Интерфейс: Utility Menu>File>Save as
9.     Запустите решение.
Команда LSSOLVE
Интерфейс Main Menu>Solution>Solve – From LS File.
10.            Конец решения.
Команда FINISH.
В методе суперпозиции мод при анализе переходных процессов записывается редуцированный файл перемещений, независимо от того, какой метод использовался для модального анализа. Если вас интересуют напряжения в конструкции, то вам необходимо проводить решение расширения. Процедура расширения решения та же самая, что для редуцированного метода. Файл Jobname.TRI необходим в том случае, если использовался редуцированный метод для модального решения. Результат решения расширения содержится в файле Jobname.RST.
Результаты содержат перемещения, напряжения, силы реакции для каждой временной точки, для которой было получено расширенное решение с использованием постпроцессоров POST26 и POST1.

6. 12 Динамический анализ предварительно напряженных конструкций
Динамический анализ предварительно напряженных конструкций позволяет рассчитывать динамическую реакцию систем, например, учитывающих тепловое расширение с остаточными тепловыми напряжениями. Динамический анализ предварительно напряженных конструкций зависит от типа переходного процесса.
6.12.1 Динамический анализ предварительно напряженных конструкций полным методом.
Вы можете включить эффекты предварительного напряжения в полном динамическом анализе с помощью приложения предварительных нагрузок в статическом шаге нагрузки, не убирая их в последующих шагах. Процедура состоит из двух основных шагов:
1.     Постройте вашу модель, войдите в SOLUTION и определите тип анализа (Переходный анализ) [ANTYPE,TRANS].

Приложите все предварительные нагрузки;
Выключите эффекты интегрирования по времени [TIMINT,OFF];
Включите эффекты упрочнения [SSTIF,ON];
Установите время, равное некоторой малой фиктивной величине [TIME];
Запишите первый шаг нагрузки в файл Jobname.S01.

Если эффекты предварительного нагружения развиваются в результате нелинейного поведения конструкции (как в случае остаточных тепловых напряжений в отливке), может понадобиться несколько шагов нагрузок для определения предварительного статического напряжения. В случае геометрической нелинейности (эффекта больших перемещений) вы можете учесть эффект предварительного напряжения командой [NLGEOM,ON].
2.     Для всех последующих шагов нагрузки включите эффекты интегрирования [TIMINT,ON] и проводите полный динамический анализ, как описано выше. Записав все шаги нагрузки в файл [LSWRITE] вы можете инициировать решение с несколькими шагами нагрузки.
6.12.2 Динамический анализ предварительно напряженных конструкций редуцированным методом.
Динамический анализ предварительно напряженных конструкций редуцированным методом требует, чтобы вы сначала нагрузили вашу модель в отдельном статическом анализе.

При этом предполагается, что напряжения, зависящие от времени (в переходном процессе) будут существенно меньше, чем напряжения от предварительного нагружения. Если это не так, то вам необходимо использовать полный динамический анализ.
1.     Постройте модель и получите статическое решение с эффектами предварительного напряжения [PSTRES,ON].
2.     Повторно войдите в SOLUTION и получите решение задачи редуцированного переходного анализа при включенном учете эффекта предварительного напряжения [PSTRES,ON]. При этом файлы Jobname.DB, Jobname.EMAT и Jobname.ESAV должны быть получены.

6.12.3 Динамический анализ предварительно напряженных конструкций методом суперпозиции мод.
При учете эффекта предварительного напряжения в методе суперпозиции мод, вы должны сначала провести модальный анализ с учетом предварительного напряжения. Если результаты модального анализа с учетом предварительного напряжения получены, то анализ переходного процесса выполняется так, как это описано выше.
7. Другие особенности анализа переходных процессов.
7.1.         Некоторые указания по выбору шага интегрирования.
Как указывалось выше, точность решения переходных процессов зависит от шага интегрирования: чем меньше шаг, тем выше точность решения. Слишком большой шаг интегрирования будет вносить ошибку в реакции высших мод. Слишком малый шаг интегрирования буде приводить к слишком большому времени счета, и необходимости большой памяти. Для расчета оптимального временного шага мы приводим пять рекомендаций:
1.     Определите частоты реакции. Временной шаг должен быть существенно меньше результирующего движения системы. Так как динамическая реакция системы может быть представлена комбинацией мод, временной шаг должен позволять анализировать высшую моду из этой комбинации. Для процедуры интегрирования по Нъюмарку найдено, что приемлемый временной шаг должен составлять двадцатую долю от периода высшей частоты.

                                   Величина шага=1/20fMAX.
Требуется меньший временной шаг, если в результате расчетов нужно определить ускорения.
На рисунке показано зависимость увеличения периода колебаний в зависимости от величины временного шага для одномассовой системы. Из графика видно, что при величине шага 1/20 от периода увеличение периода колебаний составляет менее 1%.
2.     Определите кривую нагрузки в зависимости от времени. Временной шаг должен быть достаточно малым, чтобы передать функцию нагрузки. Тенденция реакции проявляется в некотором запаздывании относительно приложенных сил, в особенности при скачкообразном изменении нагрузки, как показано на рисунке. Скачкообразное изменение нагрузки требует малых временных шагов. В этом случае рекомендуется принимать величину временного шага меньше, чем 1/180f.

Рис7.1
3.     Определите контактную частоту. В задачах с использованием контактных элементов (удара) временной шаг должен быть существенно меньше, чем время взаимодействия между двумя контактирующими поверхностями. Другими словами, будут присутствовать явные потери энергии, и удар не будет абсолютно упругим. Шаг интегрирования может быть определен из контактной частоты.
                            Шаг интегрирования = 1/Nfc,
                                      Где

Здесь k жесткость зазора, m эффективная масса в зазоре, N –число точек на цикл. Для минимизации потери энергии обычно принимают N=30. Cледует принимать большее значение, если требуется находить ускорение. Для редуцированного метода и метода суперпозиции мод N должно быть по крайней мере не меньше 7.
Вы можете использовать больше, чем 30 шагов за цикл в течение удара, если период контакта и масса контакта много меньше, чем общее время переходного процесса и массы системы потому что эффект потери энергии во всей системе может быть малым.
4.     Определите распространение волны. Если вас интересуют эффекты распространения волн, временной шаг должен быть меньше, мем время распространения волны через элемент.

5.     Определите нелинейности. Для большинства нелинейных задач, требуемый временной шаг существенно зависит от вида нелинейности. Например, система имеет тенденцию к увеличению жесткости при нагрузке (например, задача больших перемещений при изменении от изгибной модели к мембранной). При этом должна быть оценка наивысшей частоты системы.
После оценки временного шага с использованием этих рекомендаций, используйте минимальное значение для расчета. Использование автоматического временного шага позволит вам доверить проблему выбора шага программе.
7.2     Автоматический временной шаг.
Автоматический выбор временного шага позволяет изменять шаг интегрирования, основываясь на частоте реакции и нелинейных эффектах. Основная польза от этой программы состоит в том, что полное число шагов интегрирования может быть снижено. Если в задаче присутствуют нелинейности, применение автоматического шага имеет дополнительные преимущества. Вы можете активизировать автоматический выбор шага командой AUTOTS .
Хотя очевидны преимущества автоматического выбора шага для всех типов анализа, могут быть ситуации, в которых может не быть преимуществ от применения автоматического шага.

Задачи, имеющие только локализованное динамическое поведение (например, турбинные лопатки и ступица в сборе), где в части системы, содержащей низкочастотную энергию, могут преобладать высокочастотные области.
Задачи с постоянным возбуждением (например, сейсмическая нагрузка), где временной шаг имеет тенденцию непрерывно изменяться, так как возбуждаются различные частоты.
Задачи с кинематическим возбуждением (как твердого тела), где вклад колебаний как твердого тела может доминировать.

7.3 Демпфирование.
Демпфирование, присутствующее в большинстве систем должно быть в динамическом анализе. В ANSYS применяются пять видов демпфирования:

Альфа и бета демпфирование (Релеевское демпфирование);
Демпфирование, зависящее от свойств материала;
Постоянное отношение демпфирования;
Модальное демпфирование;
Демпфирование элементов.

При использовании программы ANSYS/Linear Plus возможно применение только постоянного отношения демпфирования и модального демпфирования.

Вы можете выбрать более, чем одну форму демпфирования в модели. Программа будет формировать матрицу демпфирования [C], как сумму выбранных форм демпфирования.
В таблице 7.1 приведены типы демпфирования, применимые для различных видов анализа.
Таблица 7.1

Тип анализа	Альфа и Бета демпфирование [ALPHAD, BETAD]	Демпфирование, зависящее от свойств материала [MP,DAMP]	Постоянное отношение демпфирования [DMPRAT]	Модальное длемпфирование [MDAMP]	Демпфирование элементов3 [COMBIN7 и т.д.]
Статика	Нет	Нет	Нет	Нет	Нет

Продолжение табл.7.1

Модальный Без демпфирования Модальный с демпфированием	Нет5 Да	Нет5 Да	Нет5 Да	Нет Да	Нет Да
Гармонический Полный Усеченный Супер. Поз Мод
Да	Да	Да	Нет	Да
Да	Да	Да	Нет	Да
Да	Да4	Да	Да	Нет
Переходный Полный Редуцированный Супер. Поз Мод
Да	Да	Нет	Нет	Да
Да	Да	Нет	Нет	Да
Да	Да4	Да	Да	Нет
Спектральный SPRS MPRS2	Да1	Да	Да	Да	Нет
DDAM	Да1	Да	Да	Да	Нет
PSD	Да	Нет	Да	Да	Нет
Устойчивость	Нет	Нет	Нет	Нет	Нет
Подконструкции	Да	Да	Нет	Нет	Да

Примечание к таблице 7.1
1.     Только b демпфирование
2.     Демпфирование используется только для комбинаций мод, а не для расчета коэффициентов мод.
3.     Включая матрицу демпфирования суперэлемента.
4.     Если преобразуется к модальному демпфированию раскрытием мод
5.     Эффективное отношение демпфирования определяется для спектрального анализа.
Альфа и бета демпфирование применяется для определения матрицы демпфирования по Рэлею.

Матрица демпфирования определяется с использованием матрицы масс и матрицы жесткости:

Команды ALPHAD и BETAD используются для определения a и b как десятичных чисел. Значения a и b, как правило, не известны заранее, но они могут быть определены из коэффициентов модального демпфирования

-отношение действительного демпфирования к критическому демпфированию отдельной i-той моды. Если

- собственная круговая частота i -той моды, то a и b должны удовлетворять соотношению:

Во многих практических случаях альфа демпфирование (или массовое демпфирование) может игнорироваться (a=0). В этих случаях вы можете определить b из известных значений

как

.
Для определения коэффициентов a и b при заданном отношении демпфирования x обычно принимается, что сумма a и b членов примерно постоянна в частотном диапазоне.(Рис. 7.2). Таким образом, при данной x и частотном диапазоне от

до

- коэффициенты a и b могут быть определены из системы двух уравнений.

Рис.7.2
Альфа демпфирование может приводить к неверным результатам, если большая масса была искусственно введена в модель. Один общий пример, когда искусственно большая масса вводится в основание модели для возможности ввода спектра ускорений. (Вы можете использовать большие массы для преобразования спектра ускорений в спектр сил). Демпфирующий коэффициент альфа, который умножается на матрицу масс, будет давать искусственно завышенную силу демпфирования в таких системах, что приводит к ошибкам во входном спектре и в определении реакции системы.
Бета демпфирование и демпфирование материала может приводить к искаженным результатам в нелинейном анализе. Эти коэффициенты демпфирования умножаются на матрицу жесткости, которая постоянно изменяется в нелинейных задачах. Результирующее изменение в демпфировании может быть иногда противоположным действительному изменению демпфирования, что может исказить физическую сущность задачи.

Например, из опыта известно, что в физических системах, которые размягчаются при пластической деформации, обычно соответственно повышается демпфирование при развитии пластического течения. В модели ANSYS, имеющей бета демпфирование, будет снижение демпфирования при развитии пластической деформации.
Демпфирование, зависящее от свойств материала, позволяет вам определять бета демпфирование как свойства материала [MP,DAMP]. Следует отметить, что в спектральном анализе вводится демпфирующее отношение, зависящее от свойств материала x, а не b. Еще отметим, что для элементов, в которых возможны несколько материалов, такие, как SOLID46, SOLID65, SHELL91, SHELL99, b может быть определен для всего элемента, а не для каждого материала в элементе. В этом случае b определяется из свойств материалов элементов с помощью команды MAT.
Постоянное отношение демпфирования – наиболее простой путь определения демпфирования для системы. Он представляет собой отношение действительного демпфирования к критическому значению и вводится как десятичная дробь командой DMPRAT. Это возможно только в спектральном анализе, гармоническом анализе и в методе суперпозиции мод в анализе переходных процессов.
Модальное демпфирование дает вам возможность вводить различное отношение демпфирования для различных мод колебаний. Это возможно только спектрального анализа и для метода методе суперпозиции мод в анализе переходных процессов.
Демпфирование элементов вводится для элементов с вязким демпфированием, таких как COMBIN7, COMBIN14, COMBIN37, COMBIN40 и т. д.
8. СПЕКТРАЛЬНЫЙ АНАЛИЗ.
Спектральный анализ – это решение задачи с использованием результатов модального анализа для расчета перемещений и напряжений в модели. Он в основном используется вместо временного анализа для определения реакции при случайных нагрузок или нагрузках, зависящих от времени, таких как землетрясение или ветровые нагрузки, нагрузки от морских волн, воздействие от реактивного двигателя, и т. д.
Спектр это график спектральной величины в функции от частоты, что определяет интенсивность и спектральный состав динамических нагрузок.

Возможны три типа спектрального анализа:

Спектр реакции;

-Единственный спектр реакции (SPRS)
-Множественный спектр реакции (MPRS)

Метод динамического проектирования (DDAM)
Метод спектральной плотности мощности (PSD).

8.1 Виды спектрального анализа.
8.1.1 Спектр реакции.
Спектр реакции представляет реакцию систем с одной степенью свободы, на нагрузку, зависящую от времени. Это график реакции в функции от частоты, где в качестве реакции может быть принято перемещение, скорость, ускорение или сила. Возможны два типа спектрального анализа реакции: единственный спектр реакции и множественный тип реакции.
При анализе единственного спектра реакции вы выбираете одну спектральную кривую (или семейство кривых) в ряде точек модели, например в опоре.
При анализе множественного спектра реакции вы выбираете различные спектральные кривые в различных точках.
8.1.2 Метод динамического проектирования.
Метод динамического проектирования – это технология, используемая для оценки ударной сопротивляемости судового оборудования. Технология по существу является спектральным анализом реакции, в котором спектр получается из серии эмпирических уравнений и ударных проектных таблиц, полученных в Американской Национальной исследовательской лаборатории. Отчет NRL-1396.
8.1.3    Метод спектральной плотности.
Спектральная плотность мощности – это статистическая величина, для которой в качестве предела определена среднеквадратичная величина случайной переменной. Она используется в анализе случайной вибрации, в котором мгновенное значение реакции может быть определено только по функции вероятностного распределения, показывающей вероятность нахождения случайной величины в некотором интервале.
График спектральной плотности может строиться в функции частоты для перемещения, скорости, ускорения или силы. Математически, площадь под кривой равна дисперсии (или среднему квадрату).
8.2       Последовательность действий при решении задачи спектрального анализа.

1.     Построение модели
2.     Получение модального решения
3.     Получение спектрального решения
4.     Расширение мод
5.     Комбинация мод
6.     Просмотр результатов.
Модальное решение должно быть получено перед расчетом спектра, формы мод и частоты используются в спектральном анализе. Производя спектральное решение перед раскрытием мод, вы можете раскрыть только те моды, которые требуются для финального решения.
Построение модели.
В этом шаге вы определяете имя задачи, заголовок задачи, затем используя препроцессор определяете тип элементов, реальные константы, свойства материалов и геометрию модели.
Учитывается только линейное поведение в спектральном анализе. Нелинейные элементы (если они есть) представляются как линейные. Например, если вы включаете контактные элементы, их жесткость рассчитывается на начальном этапе, и не изменяется.
Модуль упругости (или жесткость в некоторой форме) и плотность (или масса) должны быть обязательно заданы. Свойства материала могут быть линейные, изотропные или ортотропные, постоянные или зависящие от температуры, но нелинейные свойства игнорируются.
Получение модального решения.
Собственные частоты и формы мод необходимы для получения спектрального анализа.

Используйте метод подпространства, блочный или редуцированный. Другие методы не подходят для спектрального анализа.
Число полученных мод должно быть достаточным для характеристики реакции системы в интересующем вас частотном диапазоне.
Если вы используете метод интерфейса, выбирайте NO на диалоговом меню раскрытия мод [MODOPT], так что моды не раскроются в это время, но могут быть раскрыты отдельно в соответствующем шаге решения. В этом случае нужно выбирать YES для раскрытия всех мод.
Если вы используете демпфирование, зависящее от свойств материалов, вы должны это выбрать в модальном анализе.
Необходимо закрепить те степени свободы, где вы хотите приложить входной спектр основания.

Получение спектрального решения.

Файл формы мод (Jobname.MODE) из модального анализа должен быть получен и база данных должна содержать данные этой модели.
1. Войдите в режим решения:
Команда /SOLU или интерфейс Main Menu>Solutions
2. Определите тип анализа и его опции.
Таблица 8.1
Тип анализа и опции

Опции	Команды	Действия в интерфесе
New Analysis	ANTYPE	Main Menu>Solutions>Analys Type>New Analys
Analys Type: Spectrum	ANTYPE	Main Menu>Solutions>Analys Type>New Analys>Spectrum
Тип спектра:SPRS	SPOPT	Main Menu>Solutions>Analys Options
Число мод для решения	SPOPT	Main Menu>Solutions>Analys Options

Точность решения существенно зависит от числа используемых мод: чем больше число мод, тем выше точность.
3. Определите опции шагов нагрузки. Возможны следующие опции для однофакторного спектрального анализа.
Опции шагов нагрузки
Таблица 8.2

Опция	Команда	Действия в интерфейсе
Опции спектра
Тип спектра реакции	SVTVP	Main Menu>Solutions>Load Step Opt-Spectrum>Single-point-Settings
Направление возбуждения	SED	Main Menu>Solutions>Load Step Opt-Spectrum>Single-point-Settings
Зависимость спектра от частоты (спектральная кривая)	FREQ, SV	Main Menu>Solutions>Load Step Opt-Spectrum>Single-point-Freq Table/Spectr Values
Демпфирование (динамические опции)
Бета (демпфирование, пропорциональное жесткости	BETAD	Main Menu>Solutions>Load Step Opt>Time/Frequens>Damping
Постоянное отношение демпфирования	DMPRAT	Main Menu>Solutions>Load Step Opt>Time/Frequens>Damping
Модальное демпфирование	MDAMP	Main Menu>Solutions>Load Step Opt>Time/Frequens>Damping

Опции спектра.
Опции спектра содержат следующее:

Тип спектра [SVTYP].

Тип спектра может быть перемещение, скорость, ускорение, сила или спектральная плотность.

Все спектры за исключением силы представляют собой сейсмически спектры и действуют на опорах. Спектр силы прикладывается на не опорных узлах с помощью команд F или FK и по направлению меток FX, FY, FZ. Спектральная плотность [SVTYP,4] внутренне преобразовывается в спектр перемещений и ограничивается шириной полосы частот.

Направление воздействия.
Спектральная кривая [FREQ, SV].

Команды FREQ, SV используются для определения спектральной кривой. Вы можете определить семейство спектральных кривых, каждая кривая для различного отношения демпфирования. Используйте команду STAT для печати текущих значений кривых. Другая команда ROCK позволяет вам определить спектр качаний.
Демпфирование (динамические опции).
Если вы выбрали более, чем одну форму демпфирования, ANSYS будет рассчитывать эффективное отношение демпфирования на каждой частоте. Спектральное значение этого эффективного отношения демпфирования будет затем рассчитываться методом интерполяции на спектральной кривой. Если демпфирование не определено, будет использоваться спектральная кривая с наивысшим демпфированием.
4.     Запустите решение.
Main Menu>Solution>Solve-Current LS
Выход решения включает таблицу действующих факторов. Таблица действующих факторов содержит коэффициенты мод (принятых по наинизшему отношению демпфирования) и распределение масс для каждой моды. Для получения максимальной реакции каждой моды (модальной реакции) нужно умножить форму моды на модальный коэффициент. Вы можете сделать это восстановлением коэффициентов мод командой GET и использованием их в качестве масштабного фактора в команде SET.
5.     Повторите шаги 3 и 4 для дополнительных спектров реакции, если это необходимо. Заметим, что решение не записывается в файл с расширением RST в это время.
6.     Выйдите из процессора.
8.3       Расширение мод.
1.     Нажмите на кнопку «YES» на диалоговом окне расширения мод (Expansion Pass).

Команда MXPAND.
Интерфейс: Main Menu>Solution>New Analys-Modal Expansion Pass-On > L.S Opt-Expansion Pass>Single Expand-Modal-Expand Modes
Вы должны раскрывать моды, не зависимо от того, какой метод используется: подпространства, блочный или редуцированный.

Селективно раскрыты, могут быть только значительные моды. (См. использование поля SIGNIF в команде MXPAND). Если вы используете интерфейс и хотите выборочно раскрыть моды, Выберите «NO» в диалоговом окне раскрытия мод для опций модального анализа [MODOPT].
Только раскрытые моды используются для операции комбинации мод.
Если вас интересуют напряжения, вы должны здесь запросить расчет напряжений. По умолчанию, напряжения не определяются при раскрытии мод, это означает, что напряжения не определяются для спектрального анализа.
Если вы хотите раскрыть все моды, вы можете включить шаг раскрытия мод в модальном анализе командой MXPAND. Если вы используете интерфейс и хотите раскрыть все моды, выберите «YES» в диалоговом окне для модального анализа. Но если вы хотите раскрыть только значительные моды вы должны рассматривать раскрытие мод как отдельное решение после спектрального анализа. Заметим, что решение модального анализа записывается в результирующий файл Jobname.RST, только если раскрытие мод закончено.

8.4       Комбинирование мод.
1. Войдите в режим «решение».
Main Menu>Solutions.
2.     Определите тип анализа.
Main Menu>Solutions>Analys Type>New Analys
Выберите тип анализа «spectrum»
3.     Выберите один из способов метода комбинаций мод для спектрального анализа:

Квадратный корень из суммы квадратов (SRSS);
Полная квадратичная комбинация (CQC);
Двойная сумма (DSUM);
Группирование (GRP);
Суммирование по способу военно-морской исследовательской лаборатории. (NRLSUM).

Для определения метода комбинаций мод используются команды:
SRSS
CQC
DSUM
GRP
NRLSUM
Интерфейс: Main Menu>Solution>New Analys->Spectrum >Analysis Opt-SPRS> Load Step Opt-Spectrum>Spectrum-Single Point-Mode Combin.

Эти команды позволяют считать различные типы реакций:

Перемещение (метка=DISP);
Скорость (метка =VELO);
Ускорение (метка =ACEL)

Примечание: вы должны определить демпфирование, если вы используете метод CQC.
4. Запустите решение.
Main Menu>Solution>Solve-Current LS
Результаты решения записываются в файл Jobname.MCOM Чтение этого файла в постпроцессоре POST1 производится с использованием Jobname.RST из шага раскрытия мод. Файл Jobname.MCOM содержит команды POST1, комбинирующие максимальные модальные реакции с использованием выбранного способа комбинирования мод для расчета предельных реакций системы.

Если вы выбрали перемещение в качестве типа реакции, то перемещения и напряжения комбинируются для каждой моды;
Если вы выбрали скорость в качестве типа реакции, то скорость и напряжения комбинируются для каждой моды;
Если вы выбрали ускорение в качестве типа реакции, то ускорения и напряжения комбинируются для каждой моды;

5.     Выйдите из процессора.
8.5       Просмотр результатов.
Результаты спектрального анализа записываются в файл Jobname.MCOM в форме команд постпроцессора POST1. Эти команды рассчитывают предельные реакции системы комбинацией максимальных модальных реакций в некотором виде ( в соответствии с выбранным методом). Предельные реакции состоят из предельных перемещений (или скоростей или ускорений), и если помещены в результирующий файл при шаге раскрытия мод, предельные напряжения, деформации и силы реакции.
Вы можете использовать генеральный постпроцессор POST1 для просмотра результатов.
Примечание: Если вы хотите непосредственно комбинировать действующие напряжения (S1, S2, S3, SEQV, SI) из результирующего файла, введите команду SUMTYPE, PRIN перед чтением файла Jobname.MCOM.
1.     Прочтите команды из файла Jobname.MCOM.
Команда /INPUT, например, /INPUT,FILE,MCOM.
Интерфейс: Utility Menu>File>Read Input From
2.     Просмотрите результаты.

Опция: просмотр деформированного состояния.
Команда PLDISP.
Интерфейс: Main Menu>General Postproc>Plot Results>Deformed Shape.
Опция просмотр результатов в контурном виде.
Команды PLNSOL или PLESOL.
Интерфейс: Main Menu> General Postproc>Plot Results> Contour Plot>Nodal Solu или Element Solu.
Опция просмотр результатов в векторном виде.
Команда PLVEC
Интерфейс: Main Menu> General Postproc>Plot Results> Vector Plot>Predefined
Опция табулированный листинг.
Команды: PRNSOL (решение в узлах);
PRESOL (решение в элементах);
PRRSOL (Силы реакции).
Интерфейс:
Main Menu> General Postproc>List Results> Nodal Solution
Main Menu> General Postproc>List Results> Element Solution
Main Menu> General Postproc>List Results> Reaction Solution
В постпроцессоре POST1 предусмотрено много других функций, таких как масштабирование результатов в различные координатные системы, комбинация случаев нагружения и т. д
8.6       Пример расчета простой системы.
Описание задачи.
Балка с шарнирными опорами, длиной l, массой m, распределенной по длине, подвергается вертикальной вибрации на обеих опорах. Вибрация определена как спектр перемещений. Определить перемещения узлов, усилия реакции и решение для элементов.
Исходные данные.
Модуль упругости Е=30*106psi
Масса m=0.2 ibsec2/in2
Момент инерции поперечного сечения J=1000/3 in4
Площадь поперечного сечения A=273.9726 in2.
Длина балки l=240 in
Высота сечения h=14 in.

Спектр воздействия
Частота, Гц	Перемещение, in
0.1 800	0.44 0.44

        Установка типа анализа.
1.     Utility Menu>File>Change Title
2.     Введите текст «Seismic response of beam structure» и нажмите ОК.
Определение типов элементов
1.          Main Menu>Preprocessor>Element Type>Add/Edit/Delete Откроется диалоговое меню.
2.          Нажать на Add.

Откроется диалоговое окно библиотеки элементов.
3.          В левой части выбрать «Structural Beam»
4.          В правой части нажать на « 2D elastic3».
5.          Нажать ОК. Диалоговое окно элементов закроется.
6.          Нажать на Close окна типов элементов.
Определение реальных констант.
1.     Main Menu>Preprocessor>Real Constant. Откроется диалоговая коробка реальных констант.
2.     Нажать Add. Откроется диалоговое окно типов элементов для реальных констант.
3.     Нажать ОК. Откроется диалоговое окно для элемента BEAM3.
4.     Введите 273.9726 как площадь поперечного сечения.
5.     Введите (1000/3) для момента инерции.
6.     Введите 14 для высоты балки.
7.     Нажмите на Close.
Определение свойств материала.
1.      Main Menu>Preprocessor>Material Props>Constant-Isotropic. Откроется диалоговое окно свойств материала.
2.      Нажать на ОК, выбирая по умолчанию материал номер 1.Откроется диалоговое окно изотропных свойств материала.
3.      Ввести 30e6 для модуля упругости.
4.      Ввести 73E-05 для плотности нажать ОК.
Определение точек и линии.
1.        Main Menu>Preprocessor>Modeling-Create>Keypoints> In Active Cs. Откроется диалоговое окно построения точек.
2.        Введите 1 для номера точки.
3.        Нажмите Apply выбирая по умолчанию координаты X,Y,Z равными нулю.
4.        Введите 2 как номер точки.
5.        Введите 240,0,0 для координат X,Y,Z .

6.        Нажмите ОК.
7.        Utility Menu>PlotCtrl>Numbering . Откроется диалоговая коробка нумерации.
8.        Нажать на “keypoint numbering on»
9.        Нажать ОК.
10.   Main Menu>Preprocessor>Modeling-Create>Line> Straight Line. Откроется пиковое меню
11.   Нажать на точку 1, затем на точку 2. Возникнет прямая линия между двумя точками.
12.   Нажать ОК.
Установка разбиений.
1.     Main Menu>Preprocessor>Meshing –Size Cntrls >Global – Size. Откроется диалоговое окно.
2.     Введите 40, как число делений и нажмите ОК.
3.     Main Menu>Preprocessor>Meshing –Mesh >Lines
4.     Нажмите ALL.
Установка граничных условий.
1.     Main Menu>Solutions>Loads-Apply >Structural-Displacement>On Nodes
2.     В графическом окне нажать на узел на левом конце балки.
3.     Нажать ОК.
4.     Нажать на UY.
5.     Нажать ОК.
6.     Повторить шаги 1-3 и выбрать узел на правом конце балки.
7.     В коробке нажать на UX и теперь и UX и UY будут выделены.
8.     Нажать ОК.
Определение типа анализа и опции.
1.     Main Menu>Solutions>Analys Type>New Analys
2.     Выбрать “Modal» и нажать ОК. Откроется диалоговое окно.
3.     Main Menu>Solutions>Analys Options Откроется диалоговое окно модального анализа.
4.     Выбрать по умолчанию “Subspace» как метод раскрытия мод.
5.     Введите 10 как число мод и нажмите ОК.
6.     Нажмите на кнопку раскрытия мод [MXPAND] и выбрать «NO».

7.     Нажмите ОК. Откроется диалоговое окно модального анализа.
8.     Нажмите ОК.
Решение модального анализа.
1.     Main Menu>Solution>Solve-Current LS
2.     Просмотрите информацию в окне статуса нажмите Close.
3.     Нажмите ОК на Solve Current Step.
4.     Когда решение будет получено, возникнет сообщение «Solution is done”
Установка спектрального анализа.
1.     Main Menu>Solutions>Analys Type>New Analys
2.     Откроется диалоговая коробка с предупрежающей надписью “Изменение типа анализа правильно только внутри первого временного шага” Нажать ОК. Нажать на CLOSE.
3.     Нажать на «Spectrum» и нажать ОК.
4.     Выбрать по умолчанию единственный спектр реакции (SPRS) и ввести 10 для числа мод в решении.
5.     Нажать на диалоговую кнопку, выбирая YES для расчета напряжений. Нажать ОК.
6.     Main Menu>Solutions>Load Step Opt-Spectrum>Single-point-Settings. Откроется диалоговое окно.
7.     Выбрать «Seismic displac”.
8.     Введите 0,1,0 для выбора направления воздействия.
Определение величины спектра из таблицы частот.
1.     Main Menu>Solutions>Load Step Opt-Spectrum>Single-Point-Freq Table.
2.     Введите 0.1 для FREQ1 и 800 для FREQ2 и нажмите ОК.
3.     Main Menu>Solutions>Load Step Opt-Spectrum>Single-Point-Spectr Values. Откроется диалоговое окно Значение спектра - Отношение демпфирования.
4.     Нажмите ОК, выбирая по умолчанию без демпфирования. Откроется диалоговая коробка значения спектра.
5.     Введите 0.44 и 0.44 для FREQ1 и FREQ2.
6.     Нажмите ОК.
Решение спектрального анализа.
1.     Main Menu>Solution>Solve-Current LS

2.     Просмотрите информацию в окне статуса нажмите Close.
3.     Нажмите ОК на Solve Current Step.
4.     Когда решение будет получено, возникнет сообщение «Solution is done”
Установка шага расширения мод.
1.     Main Menu>Solutions>Analys Type>New Analys
Откроется диалоговая коробка с предупрежающей надписью “Изменение типа анализа правильно только внутри первого временного шага” Нажать ОК. Нажать на CLOSE.
2.     Нажать на «Modal» и нажать ОК.
3.     Main Menu>Solutions>Expansion Pass
4.     Нажать на диалоговую кнопку в положение ON и нажать ОК.
Раскрытие мод.
1.     Main Menu>Solution>Load Step Opts-Expansion Pass>Single Expand-Expan Modes.
2.     Введите 10 для числа мод и введите 0.005 для порога важности.
3.     Нажмите на кнопку результатов элементов, выбирая YES.
4.     Нажмите ОК.
Выполнение раскрытия мод.
1.     Main Menu>Solution>Solve-Current LS
2.     Просмотрите информацию в окне статуса и нажмите Close.
3.     Нажмите ОК.
4.     Когда решение будет получено, возникнет сообщение «Solution is done”
Установка комбинирования мод для спектрального анализа.
1.     Откроется диалоговая коробка с предупрежающей надписью “Изменение типа анализа правильно только внутри первого временного шага” Нажать ОК. Нажать на CLOSE.
2.     Нажать на Spectrum и нажать ОК.
3.     Main Menu>Solutions>Analys Options. Откроется диалоговое окно спектрального анализа.
4.     Выбрать по умолчанию единственный спектр реакции (SPRS). Нажать ОК.
Выбор метода раскрытия мод.
1.      Main Menu>Solutions>Load Step Opt-Spectrum>Single-Mode Combine. Откроется диалоговое окно.

2.      Выбрать SRSS как метод комбинирования мод.
3.      Ввести 0.15 как порог важности.
4.      Выбрать перемещения как тип выходных данных. Нажать ОК.
Комбинирование мод
1.     Main Menu>Solution>Solve-Current LS
2.     Просмотрите информацию в окне статуса и нажмите Close.
3.     Нажмите ОК.
4.     Когда решение будет получено, возникнет сообщение «Solution is done”
Постпроцессор: вывод на печать узловых и элементных данных, реакций.
1.     Main Menu> General Postproc>List Results> Results Summary. Откроется окно листинга.
2.     Просмотрите информацию и нажмите Close.
3.     Utility Menu>File>Read Input From. Откроется диалоговое меню чтения файлов.
4.     В левой части диалогового окна выбрать директорию, содержащую ваши результаты.
5.     В правой части окна выбрать файл Jobname.mcom.
6.     Нажать ОК.
7.     Main Menu> General Postproc>List Results> Nodal Solution.
8.     В левой части диалогового окна выбрать по умолчанию DOF solution, а в правой части «All DOFs DOF»
9.     Откроется окно листинга. После просмотра нажать Close.
10.            Main Menu> General Postproc>List Results> Element Solution. Откроется диалоговое окно решения элементов.
11.            В левой части диалогового окна выбрать «Line Elem Result» и выбрать «Structural ELEM» в правой части. Нажать ОК.
12.            Откроется листинг. После просмотра нажать Close.
13.            Main Menu> General Postproc>List Results> Reaction Solution.

14.            В левой части меню выбрать «All struc fors F» и нажать ОК.
15.            Откроется листинг. После просмотра нажать Close.
8.7 Как выполнить анализ случайных колебаний.
Процедура анализа случайных колебаний состоит из шести основных шагов:
1.     Построение модели;
2.     Получение модального решения;
3.     Раскрытия мод;
4.     Получение спектрального решения;
5.     Комбинирование мод;
6.     Просмотр результатов.
Первые два шага – те же самые, что для спектрального анализа. Анализ случайных колебаний не предусмотрен для программы ANSYS/Linear Plus.
При использовании интерфейса, в диалоговом окне модального анализа [MODOPT] содержатся опции для раскрытия мод [MXPAND]. Нажмите «YES» для раскрытия мод. Здесь процедура получения модального анализа и раскрытия мод объединена в один шаг.
8.7.1 Раскрытие мод.
Вы должны раскрыть моды, полученные методом подпространства, блочным методом и редуцированным методом. При этом необходимо учесть некоторые особенности:

Только раскрытые моды учитываются в шаге комбинирования мод;
Если вас интересует вычисление напряжений, возникающих от действия спектра, их нужно «заказать» здесь.
Раскрытие мод может быть отдельным шагом решения, или может быть включено в модальный анализ.
В конце шага раскрытия мод выйдите из режима «решение» командой FINISH.

8.7.2.Получение спектрального решения
Для получения спектрального решения база данных должна содержать данные модели и следующие файлы из модального анализа: Jobname.MODE,.ESAV,.EMAT,.FULL,.RST и DB.
1. Войдите в решение.
Main Menu>Solutions.
2. Определите тип анализа и опции.

Для типа спектра [SPOPT] выберите спектральную плотность мощности (PSD);
Выберите расчет напряжений (ON), если это вас интересует.

3. выберите опции шагов нагрузки.

Возможны следующие опции:
Spectrum Data

Тип спектральной плотности.

Спектральная плотность может быть задана в виде перемещения, скорости, силы, давления, ускорения. Это будет или возбуждение основания, или возбуждения узлов в шагах 4и 5. Если применяется спектральная плотность в виде давления, то давление должно быть определено в модальном анализе.
Команда: PSDUNIT.
Main Menu>Solution>Spectrum>-PSD-Setting.

Таблица спектральной плотности в функции частоты.

Команды: PSDFRQ, PSDVAL.
Интерфейс: Main Menu>Solution>Spectrum>-PSD-PSD vs Freq.
В шаге 6 описано, как применить дополнительное возбуждение от спектральной плотности.
Демпфирование (динамические опции).
Возможны следующие формы демпфирования ALPHAD, BETAD, MDAMP.

Альфа, демпфирование, пропорциональное матрице масс.

Команда ALPHAD.
Main Menu > Solution> Load Step Opts-Time/Frequenc>Damping.

Бета демпфирование, пропорциональное матрице жесткости.

Команда BETAD.
Main Menu > Solution> Load Step Opts-Time/Frequenc>Damping.

Постоянное отношение демпфирования.

Команда DMPRAT.
Main Menu > Solution> Load Step Opts-Time/Frequenc>Damping.

Частотно-зависимое отношение демпфирования.

Команда MDAMP.
Main Menu > Solution> Load Step Opts-Time/Frequenc>Damping.
4.     Приложите возбуждение от спектральной плотности мощности к выбранным узлам. Используйте значение 1.0 для обозначения точек, где прикладывается возбуждение. Значение 0.0 может использоваться для удаления спецификации. Направление возбуждения выбирается с помощью меток UX, UY, UZ команды D (при возбуждении основания) и меток FX, FY, FZ команды F при возбуждении узлов. При возбуждении узлов значение, больше, чем 1.0 может быть использовано для масштабного фактора участия. Для спектральной плотности в виде давления необходимо перенести вектор нагрузки из модального анализа [LVSCALE]. Вы можете приложить возбуждение основания только в тех узлах, что были закреплены в модальном анализе.

Команды D или DK, DL, DA для возбуждения основания.
F или FK для возбуждения узлов. LVSCALE для давления.
Интерфейс: Main Menu>Solution>-Loads-Apply>Spectrum>-BasePSD Excit-On Nodes.
5.     Рассчитайте фактор участия для возбуждения спектральной плотностью. Используйте поле TBLNO (номер таблицы) какая именно таблица спектральной плотности будет применяться и поле Ecxit для для обозначения, будет ли возбуждаться основание или узел.
Команда PFACT.
Интерфейс: Main Menu>Solution>-Load Step Opts - Spectrum>-PSD- Calculate PF
6.     Если вам необходимо приложить несколько воздействий в виде спектральных плотностей к одной и той же модели, повторите шаги 3, 4, 5 для каждой дополнительной спектральной плотности. Затем определите, если это необходимо степень корреляции между возбуждениями, используя следующие команды:
COVAL для взаимной спектральной плотности;
QDVAL для квадратичных спектральных значений;
PSDSPL для пространственных соотношений;
PSDWAV для соотношений при распространении волны.
Интерфейс: Main Menu>Solution>-Load Step Opts - Spectrum>-PSD- Correlation
Когда вы используете команды PSDSPL или PSDWAV вы должны соответственно использовать SPATIAL или WAVE в команде PFACT.
7.     Выбор управления выходными параметрами.
Только команда PSDRES обеспечивает правильный контроль выходных данных и запись результирующего файла. Может быть выполнено три вида расчета: перемещение, скорость, ускорение. Каждое из них может быть определено относительно основания или абсолютно.
Команда PSDRES.
Интерфейс: Main Menu>Solution>-Load Step Opts - Spectrum>-PSD- Calc Controls.
В таблице 8.3 приведены возможные настройки решения.
Таблица 8.3

Решение	Параметры	Форма
Перемещения (метка DISP в команде PSDRES)	Перемещения, напряжения, деформации, силы	Относительное, абсолютное, или оба
Скорость (метка VELO в команде PSDRES)	Скорость, скорость напряжения, и т. д.	Относительное, абсолютное, или оба
Ускорение (метка ACEL в команде PSDRES)	Ускорение, ускорение напряжения и т. д.	Относительное, абсолютное, или оба

8.     Запустите решение.
Main Menu>Solution>Solve-Current LS.
9.     Выйдите из режима решения.
8.7.3    Комбинирование мод.
1.     Войдите в решение.
Main Menu>Solutions.
2.     Определите тип анализа.
Опция NEW Analysis [ANTYPE]
Выберите тип анализа - spectrum.
3.     Только PSD mode combination метод является допустимым для анализа случайных колебаний. Этот метод позволяет рассчитывать перемещения в форме одной сигмы, напряжения и т. д. в модели. Если вы не введете команду PSDCOM, программа не будет считать параметры в виде одной сигмы.
Команда PSDCOM
Интерфейс: Main Menu>Solution>-Load Step Opts - Spectrum>-PSD- Mode Combin.
Поля SIGNIF и COMODE часто используются для снижения числа мод. Если вы хотите испробовать эту опцию необходимо распечатать модальную ковариационную матрицу для начального получения относительной комбинации мод.
4. Запустите решение.
Main Menu>Solution>Solve-Current LS.
5.Выйдите из режима решения.
8.7.4    Просмотр результатов.
Результаты анализа случайных колебаний записываются в результирующий файл Jobname.RST. Они состоят из следующих данных:
1.     Раскрытые формы мод из модального анализа.
2.     Статическое решение при возбуждении основания. [PFACT,,BASE].
3.     Следующие данные, если на этапе комбинации мод введена команда [PSDCOM] и сделаны установки команды [PSDRES].

1s перемещение (напряжения, деформации, силы);
1s скорость и т. д.
1s ускорение и т. д.

Вы можете просмотреть эти результаты в постпроцессоре POST1, затем рассчитать выходную спектральную плотность в постпроцессоре POST 26.
Для просмотра результатов в POST1 вы сначала должны понять, как эти данные организованы в результирующем файле. Организация файла приведена в таблице 8.4.
Таблица 8.4

Шаг нагрузки	Подшаг	Комментарии
1	1 2 3	Раскрытая мода 1 Раскрытая мода 2 Раскрытая мода 3
2 Возбуждение основания	1 2 3	Единичное статическое решение для таблицы СПМ 1 Единичное статическое решение для таблицы СПМ 2
3	1	1 сигма перемещение
4	1	1 сигма скорость
5	1	1 сигма ускорение

Примечание: В шаге 2 можно выбрать возбуждение узлов.
1.     Прочитайте набор результатов в базу данных. Например, для чтения 1s перемещения введите команду SET,3,1.
Интерфейс: Main Menu>General Postproc>-Read Results-First Set
2.     Можно использовать те же опции, что для спектрального анализа.
Примечание: Осреднение напряжений в узлах с помощью команды PLNSOL может не соответствовать при анализе случайных колебаний, потому что напряжения здесь понимаются в статистическом смысле.
8.7.5    Расчет выходной спектральной плотности в POST26.
Вы можете рассчитать и нарисовать выходную спектральную плотность перемещения, скорости или ускорения, если получены файлы Jobname.RST и Jobname.PSD.
1.     Войдите в постпроцессор POST26.
Команда /POST26
Интерфейс: Main Menu>TimeHist PostPro
2.     Подготовьте вектор частот. NPTS –число точек на частотной оси, добавляемых по обе стороны от собственной частоты для получения плавной кривой. (По умолчанию –5). Вектор частот принимается как переменная номер 1.
Команда STORE, PSD,NPTS
Интерфейс: Main Menu>TimeHist PostPro>Store Data.
3.     Определите переменные (перемещения, напряжения и т. д. ).
Команды NSOL, ESOL.
Интерфейс: Main Menu>TimeHist PostPro>Define Variables.
4.     Расчет выходной спектральной плотности и сохранение его в выбранных переменных.
Команда RPSD.
Интерфейс: Main Menu>TimeHist PostPro>Calc Resp PSD.
8.7.6    Вычисление ковариационных функций в POST26
Вы можете вычислить ковариацию между двумя переменными, записанными в результирующий файл (перемещениями, скоростями, ускорениями), если имеются файлы Jobname.RST и Jobname.PSD.
1.     Войдите в постпроцессор POST26.
Команда /POST26
Интерфейс: Main Menu>TimeHist PostPro
2.     Определите переменные, в которых содержатся интересные для вас данные.

Main Menu>TimeHist PostPro>Define Variables.
3.     Рассчитайте вклад каждой компоненты (относительно абсолютной реакции) и сохраните их в выбранной переменной. Команда PLVAR может быть использована для рисования модальных вкладов (относительно реакции), псевдостатической и смешанной части в ковариационной функции.
Команда CVAR.
Main Menu>TimeHist PostPro>Calc Covarince.
4.     Получение ковариаций.
Команда *GET,NameVAR1,n,EXTREM,CVAR.
Интерфейс: Utility Menu>Parameters>Get Scalar Data

8.8         Как выполнить анализ множественного спектра реакции.
Процедура для определения множественного спектра реакции та же самая, что для случайной вибрации со следующими отличиями:

Выберите MPRS вместо PSD как тип спектра в команде [SPOPT];
Таблица спектральной плотности в функции частоты представлена как таблица спектральных значений в функции частоты;
Вы можете выбрать некоторую степень корреляции между спектрами, или считать их некоррелированными;
Определяются только относительные результаты (относительно возбуждения основания), абсолютные значения не определяются.
Поддерживаются все методы комбинирования мод, за исключением PSDCOM.
Результаты анализа множественного спектрального анализа записываются в файл Jobname.MCOM в форме команд постпроцессора POST1. Предусмотрены команды расчета предельных реакций системы комбинацией максимальных модальных реакций. Предельные реакции состоят из предельных перемещений, предельных напряжений, предельных деформаций и сил реакции.

Часть 2. Основы теории.
9. МОДАЛЬНЫЙ АНАЛИЗ

Модальный анализ используется для определения собственных частот и форм колебаний конструкции. Предполагается, что совершаются свободные незатухающие колебания:

(9.1)
Отметим, что матрица жесткости конструкции [K] может включать в себя эффект предварительного нагружения.

Для линейной системы свободные колебания будут гармоническими:

(9.2)
где

- собственный вектор представляющий i-ую форму колебаний;

- i-ая собственная круговая частота (радиан за единицу времени);
t - время.
Таким образом, матричное уравнение (9.1) принимает следующий вид:

(9.3)
Это уравнение имеет решение, кроме тривиального

только тогда, когда определитель данной системы

равен нулю, то есть:

(9.4)
Последнее уравнение и есть задача о собственных значениях. Решением уравнения (4), если n - порядок матрицы, является характеристический полином n-го порядка, который имеет n корней:

…

, где n - число степеней свободы. Эти корни являются собственными значениями уравнения. Собственные вектора

, получают путем подстановки полученных корней

в уравнение (3). Собственное значение

определяет собственную частоту системы

, а собственный вектор

- соответствующую форму колебаний (перемещение системы).
Значения собственных круговых частот

и собственных частот (f) связаны следующим соотношением:

(9.5)
где

- i-ая собственная частота (циклов в единицу времени).
Обычно собственный вектор

называются нормированными, если выполняется следующее равенство (отражающее свойство ортогональности форм собственных колебаний):

(9.6)
то есть

В другом случае собственный вектор

нормируется из условия, чтобы наибольшие его составляющие равнялись единице. Условие ортогональности форм колебаний можно объяснить как равенство нулю сил инерции i-ой формы колебаний на перемещениях k-ой формы колебаний.
При использовании метода частотной конденсации (редукции степеней свободы) n собственных векторов затем могут быть развернуты на этапе “расширения” до полного набора модальных степеней свободы конструкции:

(9.7)
где

- вектор исключаемых (вспомогательных) степеней свободы i-ой моды ( вспомогательными степенями свободы называются те степени свободы, которые будут конденсироваться с целью снижения размерности системы);

- подматрицы жесткости по вспомогательным степеням свободы и связи вспомогательных степеней свободы с удерживаемыми соответственно;

- вектор удерживаемых (основных) степеней свободы i-ой моды.
10. МЕТОД СУПЕРПОЗИЦИИ МОД

Метод суперпозиции мод использует данные о собственных частотах и формах колебаний, полученные путем проведения модального анализа, для оценки динамического отклика конструкции от нестационарных или стационарных гармонических возмущений.
Уравнения движения могут быть выражены в следующей форме:

           (10.1)
где      [M] - матрица масс системы;
[C] - матрица демпфирования системы;
[K] - матрица жесткости системы;
{u''} - вектор узловых ускорений;
{u'} - вектор узловых скоростей;
{u} - вектор узловых перемещений;
{F} - вектор прикладываемых сил, переменных во времени, который можно расписать как:
{F} = {Fnd} + s{Fs}                         (10.2)
где     {Fnd} - вектор переменных во времени узловых силы;
s - масштабный коэффициент вектора нагрузок;
{Fs} - вектор нагрузок, полученный путем модального анализа (см. далее).
Вектор нагрузки {Fs} вычислен при выполнении анализа форм колебаний. Он образуется точно так же как и вектор нагрузки подконструкции .
Следующая разработка подобна данной в книге Бате [2].
Определим набор модальных координат yi из условия, чтобы

(10.3)
где

- форма колебаний i-ой моды;
n - число используемых мод (вводится с помощью команд TRNOPT или HROPT).
Заметьте, что уравнение (10.3) препятствует использованию отличного от нуля входного перемещения, после определения yi не напрямую, а через {u}.

Обратная зависимость существует (уравнение (10.3)) для случая, где все смещения известны, но не, когда только некоторые известны. Подставив уравнение (10.3) в (10.1) получим:

(10.4)
Умножая слева на типичную форму колебаний

(10.5)
Из условия ортогональности собственных форм колебаний следует, что

(10.6) и (10.7)
В методе суперпозиции мод, разрешено только релеевское или постоянное демпфирование вследствие того, что

(10.8)
Применяя эти условия к уравнению (10.5) останутся только члены при

(10.9)
Коэффициенты

определяются как следующие:
А. Коэффициент

:
При условии нормирования (17.3-6) -

(10.10)
В. Коэффициент

:
Член демпфирования основан на обработке модальных координат, как отдельных систем с одной степенью свободы (то есть независимых уравнений 15.11-1) для которой

(10.11)
и

(10.12)
Рисунок 10.1 - Осциллятор с одной степенью свободы
Из уравнения (10.12) можно определить

(10.13)
Из Тси (68)

(10.14)
где

- доля критического демпфирования для j-ой моды
и

где

- собственная круговая частота для j-ой моды
Объединение уравнения (10.13) с уравнениями (10.15) и (10.11)

                     (10.16)
          С. Коэффициент yj
                   Из уравнения (10.3), то есть из

(10.17)
Перемножим слева на

(10.18)
Подставим уравнение (10.10) для масс -

(10.19)
Введем условное обозначение, пусть

(10.20)
представляет правую часть уравнения (10.9). Подставим уравнения (10.10), (10.16), (10.19) и (10.20) в уравнение (10.9), и получим уравнение движения для модальных координат:

(10.21)
Поскольку j представляет любую моду, уравнение (10.21) представляет n независимых друг от друга уравнений для n неизвестных yj. Преимущество разъединенной системы состоит в том, что вся в вычислительном отношении дорогая матричная алгебра была сделана в собственном решающем устройстве, и длинные переходные режимы могут быть проанализированы недорого в главных координатах с помощью уравнения (10.21). В гармоническом анализе, частоты могут быть отсканированы быстрее, чем методом редуцированного гармонического отклика. Значения yi преобразуется назад в геометрические перемещения {u} (отклик системы на нагрузку), используя уравнение (10.3). То есть отдельные модальные отклики yi накладываются друг на друга, чтобы получить фактический отклик, отсюда название "суперпозиция мод". Если анализ форм колебаний был выполнен, используя метод конденсации (MODOPT, REDUC), то матрицы и векторы нагрузки в вышеупомянутых уравнениях будут содержать главные (удерживаемые) степени свободы (то есть {u}).
10.1 Модальное демпфирование
Модальное демпфирование,

- объединение нескольких входов демпфирования ANSYS.

                             (10.22)
где      a - множитель инерционного демпфирования (вводится командой ALPHAD)
b - множитель конструкционного демпфирования (вводится командой BETAD)
x - коэффициент постоянного демпфирования (вводится командой DMPRAT)
xmj - коэффициент модального демпфирования (вводится командой MDAMP)
Из-за предположения в уравнении (10.8), явное демпфирование в таких элементах как COMBIN14 не позволяется процедурой суперпозиции форм колебаний.
11. СПЕКТРАЛЬНЫЙ АНАЛИЗ
          Поддерживаются два типа спектрального анализа: детерминированный метод спектрального отклика и недетерминированный метод случайных колебаний. Допускается возбуждение в опорах (например, сейсмическое воздействие) и возбуждение в точках, удаленных от опор.

Существуют четыре вида спектрального анализа:

однофакторный спектральный анализ;
многофакторный спектральный анализ;
расчетно-экспериментальный метод динамического анализа;
метод спектральной плотности мощности.

Однофакторный спектральный анализ предполагает использование одной и той же спектральной кривой (например, зависимости изменения силы от времени) для всех возбуждаемых точек.
Многофакторный спектральный анализ предполагает задание в точках возбуждения различных спектральных кривых.
Расчетно-экспериментальный метод динамического анализа используется для оценки прочности корабельного оборудования. Метод состоит в получении отклика системы на спектр, который получен на основе эмпирических уравнений и таблиц расчета на удар, представленных в отчете NRL-1369 Лаборатории научных исследований военно-морских сил США.
Метод спектральной плотности мощности представляет собой вероятностный подход к нахождению спектрального отклика и известен как анализ случайных колебаний.
11.1 Допущения и ограничения
1.     Конструкция является линейной.
2.     Для однофакторного спектрального анализа и расчетно-экспериментального метода динамического анализа возмущение на конструкцию задается спектром с известным направлением и частотными составляющими, воздействующими равномерно на все опорные точки или на заданные удерживаемые (главные) не опорные степени свободы (при использовании метода частотной конденсации).
3.     Для многофакторного спектрального и спектральной плотности мощности видов анализа, конструкция может возмущаться различными входными спектрами с приложением их к различным опорным точкам и не опорным (свободным от связей) узлам. Можно задавать до десяти различных входных спектров.
11.2 Описание анализа

Спектральный анализ возможен при выборе типа анализа (ANTYPE, SPECTR) и если предварительно был выполнен модальный анализ.

Если нужно объединение мод, то требуемые моды могут быть получены путем "расширения" (восстановления), как описано в разделе 17.3 (при применении метода частотной конденсации).
Поддерживаются четыре опции - однофакторный спектральный анализ (SPOPT, SPRS), расчетно-экспериментальный метод динамического анализа (SPOPT, DDAM), метод спектральной плотности мощности (SPOPT, PSD) и многофакторный спектральный анализ (SPOPT, MPRS). Каждая опция подробно описывается далее.
11.3 Однофакторный спектральный анализ (SPOPT, SPRS)
Поддерживаются два вида возмущений: заданное на опоры (кинематическое возмущение, например, сейсмическое) и в зонах удаленных от опор (силовое возмущение). Все требуемые данные смотри в таблице 11.1
Таблица 11.1 Типы спектральной нагрузки

	Опции возмущений
Опорное возмущение	Возмущение удаленное от опор
Спектр на входе	Таблица, характеризующая спектр (команды FREQ и SV)	Таблица множителей амплитуды (команды FREQ и SV)
Ориентация нагрузки	Направляющий вектор, вводимый командой SED	Направления X, Y и Z, выбранные как опции FX, FY, FZ команды F
Распределение нагрузок	Равномерное на все опорные точки	Амплитуда в направлении X, Y, Z выбирается как VALUE команды F
Тип входа	Скорость, Ускорение, Перемещение	Сила
KSV из команды SVTYP	0 2 3,4	1

Демпфирование
Демпфирование учитывается для каждой моды и определяется как:

(11.1)
где

- коэффициент эффективного демпфирования для i-ой моды;

- множитель конструкционного демпфирования (входное значение VALUE команды BETAD);

- не демпфированная собственная круговая частота для i-ой моды;

- коэффициент постоянного демпфирования (входное значение RATIO команды DMPRAT);

- множитель демпфирования, зависящий от свойств материала № m (входное значение DAMP команды MP);

- энергия деформации для материала № m;

- вектор перемещения для i-ой моды;

- матрица жесткости части конструкции из материала № m;

- модальный коэффициент демпфирования для i-ой моды (команда MDAMP).
Заметьте, что зависящий от материала вклад демпфирования вычисляется на этапе "расширения" (восстановления) мод, так, чтобы этот вклад от демпфирования был туда включен.
11.3 Коэффициенты вклада и модальные коэффициенты
Коэффициенты вклада для заданного направления возмущения определяется как:

- для опции расчета на кинематическое возмущение (например, сейсмическое);

- для опции расчета на силовое возмущение;
где

- коэффициент вклада для i-ой моды;

- собственный вектор, нормированный с помощью уравнения (10.6) (Nrmkey on команды MODOPT не имеет никакого эффекта);

- вектор, задающий направление возмущения;

- вектор силы на входе;

- матрица масс.
Вектор, определяющий направление возмущения имеет форму:

(11.2)
где

- возмущение степени свободы j в направлении а (а может быть равно или Х, или Y, или Z); значение

может быть определено одним из двух путей.
1. Для значения D основанного на команде SED:

где Sx , Sy , Sz - входные значения SEDX, SEDY и SEDZ, соответственно для команды SED

(11.3)
2. Для значения D основанного на командах SED и ROCK:

(11.4)

R определяется как:

(11.5)
где Сx , Сy , Сz - входные значения OMX, OMY и OMZ, соответственно в команде ROCK;

- символ, обозначающий векторное произведение;
rx = Xn - Lx
ry = Xn - Ly
rz = Xn - Lz
Xn, Yn, Zn - координаты узла n
Lx , Ly , Lz - положение центра вращения (входные значения CGX, CGY и CGZ в команде ROCK).

Вектор перемещений, скорости и ускорения для каждой моды вычисляется из собственного вектора с помощью "модального коэффициента":

(11.6)
где

метка - три поля в командах объединения мод (SRSS, CQC, GRP, DSUM, NRLSUM);

- собственная круговая частота;
Ai - модальный коэффициент (см. далее).
Модальный коэффициент вычисляется в пяти различных направлениях, в зависимости от типа возмущения (команда SVTYP).
1. Для SVTYP, 0 (возмущение прикладывается к опоре в виде скорости):

(11.7)
где Svi - спектральная скорость для i-ой моды (найденная из входного спектра скорости на частоте fi и эффективном коэффициенте демпфирования

);
fi - i-ая собственная частота (число циклов за единицу времени = wi/2p);
wi - i-ая собственная круговая частота (радиан за единицу времени).
2. Для SVTYP, 1 (возмущение прикладывается в виде силы):

(11.8)
где Sfi - спектральная сила для i-ой моды (находится из входной таблицы множителей амплитуды на частоте fi и эффективном коэффициенте демпфирования

);
3. Для SVTYP, 2 (возмущение прикладывается к опоре в виде ускорения):

(11.9)
где Sai - спектральное ускорение для i-ой моды (найденное из входного спектра ускорения на частоте fi и эффективном коэффициенте демпфирования

);
4. Для SVTYP, 3 (возмущение прикладывается к опоре в виде перемещения):

(11.10)
где Sui - спектральное перемещение для i-ой моды (найденное из входного спектра перемещений на частоте fi и эффективном коэффициенте демпфирования

);
5. Для SVTYP, 4 (спектральная плотность мощности (СПМ), читай Ванмарке (34) в списке литературы теоретического руководства)

(11.11)
где Spi - спектральная плотность мощности для i-ой моды ( получена из входной спектральной плотности на частоте fi и эффективном коэффициенте демпфирования

);

- коэффициент демпфирования (входное значение RATIO, команды DMPRAT, по умолчанию 0.01);
Интеграл в вышеупомянутом уравнении аппроксимируется как:

(11.12)
где Li = fi (в целочисленной форме);
Spj - спектральная плотность мощности оцененная на частоте (f) равной j (в вещественной форме);
Df - эффективная полоса частот для fi = 1.
Когда Svi, Sfi, Sai, Sui, или Spi требуется между табличными значениями входных частот, выполняется логарифмическая интерполяция.
Спектральные значения и модальные коэффициенты выводятся в таблицу "RESPONSE SPECTRUM CALCULATION SUMMARY" заданной входной кривой с наименьшим коэффициентом демпфирования, без эффективного коэффициента демпфирования.
12. АНАЛИЗ СЛУЧАЙНЫХ КОЛЕБАНИЙ
Метод позволяет прикладывать несколько возмущений в виде спектральных плотностей мощности (PSD) на входы системы (до десяти), которые могут быть:
1. Полностью коррелированные,
2. Некоррелированные, или
3. Частично коррелированные.
Процедура основана на статистических вычислениях каждого модального отклика, и затем их объединении (суммировании или комбинировании). Принимается, что возбуждения – стационарные случайные процессы.
12.1 Описание метода
Для частично коррелированных силовых и кинематических возмущений, полные уравнения динамического поведения конструкции разделяются на две части для неизвестных и заданных перемещений соответственно:

(12.1)
где {uf} - вектор неизвестных перемещений (от силовых возмущений);
{ur} - вектор заданных перемещений (возбуждаемых случайной нагрузкой, задается единичное перемещение);
{F} - заданное силовое возмущение (значение силы может быть отличным от единицы, при учете масштабирования от коэффициентов вклада);

{0} - вектор сил реакции, соответствующая вектору заданных перемещений {ur}.
Неизвестные перемещения могут быть расчленены на псевдо-статические и динамические части:

(12.2)
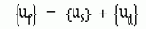
Псевдо-статические перемещения могут быть получены из уравнения (12.1) исключением первых двух слагаемых в левой части уравнения и, заменой вектора неизвестных перемещений {uf} на вектор их псевдо-статических составляющих {us}

(12.3)
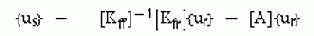
где

.
Элементы по i-ому столбцу [A] представляют собой псевдо-статические перемещения от единичных заданных перемещений возбужденных i-ой спектральной плотностью мощности (PSD). Подставим уравнения (12.3) и (12.2) в (12.1) и добавим незначительное демпфирование. Первая строка матричного уравнения (12.1) тогда может быть переписана в следующем виде:

(12.4)
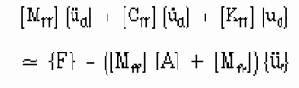
Второе слагаемое в правой части вышеупомянутого уравнения представляет эквивалентные силы, обусловленные кинематическими возмущениями.
При использовании метода суперпозиции мод уравнения (10.3) запишутся вновь как:

(12.5)
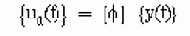
Вышеупомянутые уравнения несвязанны друг с другом и запишутся как n отдельных уравнений:

(12.6)
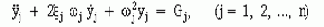
где n - число форм колебаний, выбранных для оценки;
yj - обобщенные перемещения;
wj и xj - собственные круговые частоты и модальные коэффициенты демпфирования.
Модальные нагрузки Gj определяются как:

(12.7)
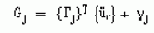
Модальные коэффициенты вклада (участия) соответствующие кинематическим возмущениям даются как:

(12.8)
и для силового возмущения

(12.9)
Формы колебаний {fj} должны быть нормированы относительно матрицы масс как в уравнении (9.6):
{f}jT[M]{f}j = {I}.
12.2 Спектральные плотности мощности отклика и среднеквадратичное значение отклика
Используя теорию случайных колебаний, отклик в виде спектральных плотностей мощности может быть вычислен от входных СПМ с помощью передаточной функцией для одной степени свободы системы Н(w), используя метод суперпозиции мод.

Отклик спектральной плотности мощности, для i-ой степени свободы дается как:
Динамическая часть

(12.10)
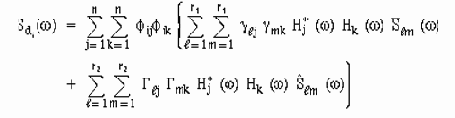
Псевдо-статическая часть

(12.11)
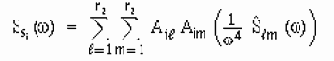
Ковариационная часть

(12.12)
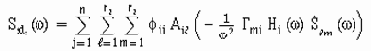
где n - число форм колебаний, выбранных для оценки;
r1 и r2 - число силовых (удаленных от опор) и кинематических СПМ-таблиц, соответственно.
Передаточные функции типа для системы с одной степенью свободы принимают различные формы в зависимости от типа вводимой СПМ и типа желательного отклика. Формы передаточных функций для перемещения как выхода перечислены ниже для различных случаев.
1. На входе - сила или ускорение:

(12.13)
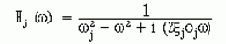
2. На входе - перемещение

(12.14)
3. На входе - скорость

       (12.15)
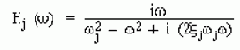
где    w - частота возбуждения
          wj – собственная круговая частота j-ой моды
          i = Ö-1 – мнимая единица.
Таким образом, анализ случайных колебаний может использоваться, чтобы показать абсолютное среднеквадратичное значение отклика неизвестных перемещений:

(12.16)
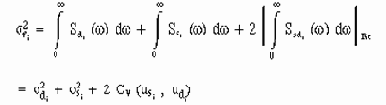
где | |Re – обозначает вещественную часть аргумента;

– дисперсия i-го псевдо-статического перемещения;

- ковариация между статическими и динамическими
перемещениями
Общая формулировка, описанная выше, дает упрощенные уравнения для некоторых ситуаций, с которыми обычно приходится сталкиваться на практике. Для полностью коррелированных силовых возмущений и идентичных заданных перемещений, нижние индексы l и m исключали бы уравнения с (12.10) до (12.12). Когда существуют только силовые возмущения, последние два члена в уравнении (12.16) не применяют, и только первый член в пределах больших круглых скобок в уравнении (12.10) обязательно будет учитываться. Для некоррелированных силовых и кинематических возмущений, взаимные спектральные плотности мощности (то есть когда l ¹ m) равны нулю, и только члены, для которых l = m в уравнениях (12.10) через (12.12) обязательно будут учтены.

Уравнения (12.10) до (12.12) могут быть перезаписаны как:

(12.17)

(12.18)

(12.19)
где

- модальные СПМ, члены, которых находятся внутри больших круглых скобок уравнений с (12.10) по (12.12)
Решение в закрытой форме получено для кусочно-линейной СПМ (PSD) в логарифмическом масштабе по обеим осям, применявшимися для вычисления каждого интеграла в уравнении (12.16) (Чен и Али (193), и Харичандран (194)). Впоследствии, дисперсия становится:

(12.20)

(12.21)

(12.22)
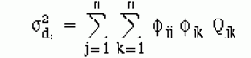
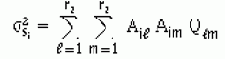
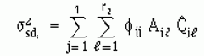
Модальные матрицы ковариации

определены в .PSD файле. Заметьте, что уравнения (12.20) до (12.22) представляют объединение мод для анализа случайных колебаний.
Дисперсия для напряжений, узловых сил или реакций может быть вычислена из уравнений, подобных с (12.20) по (12.22). Если желательно получить дисперсию напряжения, замените формы колебаний (fij) и статические перемещения (

) модальными напряжениями (

) и статическими напряжениями (

). Точно так же, если желательна дисперсия узловой силы, заменяют формы колебаний и статические перемещения модальными узловыми силами (

) и статическими узловыми силами (

). Наконец, если желательны дисперсии реакции, замените формы колебаний и статические перемещения модальными реакциями (fij) и статическими реакциями (

). Кроме того, дисперсии первых и вторых производных по времени всех величин, упомянутых выше, могут быть вычислены, используя следующие соотношения:

(12.23)

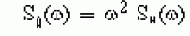
12.3 Не диагональные спектральные члены для частично коррелированных входных спектральных плотностей мощности
Для возмущений определяемых более, чем одной функцией спектральной плотности мощности (СПМ), перекрестные члены которые определяют степень корреляции между различными функциями СПМ определяют как:

(12.25)
где

- спектры СПМ на входе, которые имеют связи друг с другом;

- взаимные спектральные плотности, которые составляют вещественную часть перекрестных членов;

- составляющие спектров, которые представляют мнимую часть перекрестных членов.
Взаимная функция спектральной плотности мощности (СПМ) называется функцией когерентности:

(12.26)
где

.
Хотя вышеупомянутый пример демонстрирует взаимную корреляцию для 3 входных спектров, эта матрица может иметь диапазон в размере от 2 x 2 до 10 x 10 (то есть, максимальное число таблиц - 10).
Для частного случая, в котором все перекрестные члены являются нулевыми, входные спектры, как считают, некоррелированны. Заметим, что корреляция между силовыми и кинематическими возмущениями не позволяется.
12.4 Корреляционное пространство
Степень корреляционной связи между возбужденными узлами может также задаваться. В зависимости от расстояния между возбужденными узлами и значениями RMIN и RMAX, воздействие от спектральной плотности мощности может быть задано таким, что возбуждение в узлах может быть некоррелированно, частично коррелированно или полностью коррелированно. Если расстояние между возбужденными узлами - меньше чем RMIN, то эти два узла полностью коррелированные; если расстояние большее чем RMAX, то эти два узла некоррелированные; если расстояние находится между RMIN и RMAX, возбуждение частично коррелированно и основано на фактическом расстоянии между узлами. Рисунок ниже указывает, как соотносятся RMIN, RMAX и корреляционная связь.
Для двух возбужденных точек 1 и 2, спектральная плотность мощности была бы:

(12.27)
где:

D12 - расстояние между двумя возбуждаемыми точками 1 и 2;
So(w) - заданная на вход СПМ.

Рисунок 12.1 Сферы влияния, отражающие пространство корреляции возмущений заданных спектральной плотностью мощности
Возбуждение узла i полностью коррелированно с возбуждением узла j.

Возбуждение узла i частично коррелированно с возбуждением узла k
Возбуждение узла i некоррелированно с возбуждением узла l.
12.5 Распространение волн
Чтобы включать эффекты распространения волн по конструкции от случайного нагружения, возмущение PSD задано как:

(12.28 )
где:

(время задержки).

- Разность векторов точек возбуждения i и m.
V- Скорость распространения волны по осям X, Y и Z.

- координаты возмущенного узла l.
Допускается более чем одна одновременная волна или пространственно коррелированные входные спектральные плотности мощности, когда входное воздействие [S(w)] отражает влияние двух или более некоррелированных входных спектров. В этом случае, частичная корреляция среди заданных на входы системы спектральных плотностей мощности в настоящее время не разрешается.
12.6 Метод многофакторного спектрального анализа (SPOPT, PSD)
Анализ спектрального отклика поддерживает многофакторные кинематические и силовые возмущения, разрешая до 10-ти различных спектральных таблиц которые могут быть не связаны (некоррелированны) между собой.
Много составляющих для выполнения анализа многофакторного спектрального отклика системы уже рассмотрены в предыдущих подразделах, посвященных методу случайных вибраций. Полагая, что коэффициенты вклада

могут быть вычислены (например, из уравнения (12.8)), модальные коэффициенты для l-ой таблицы находятся как:

(12.29)
где

- интерполированная входная спектральная характеристика для l-ой таблицы j-ой собственной частоты;
Модальные коэффициенты объединяются с использованием метода квадратного корня из суммы квадратов (SRSS):

(12.30)
Формы колебаний, модальные напряжения и другие результаты, после умножения на модальные коэффициенты, затем могут быть объединены с помощью любого из доступных способов объединения мод: (квадратного корня из суммы квадратов (SRSS), полного квадратичного объединения (CQC), двойной суммы (DSUM), группирования (GRP) или методом суммирования (DDAM) Лаборатории (NRL) военно-морских сил США), как описано в предыдущих разделах, посвященных однофакторному спектральному анализу.

Содержание раздела