Богатство языка программирования
Это программа для моделирования одного шага эволюции клеточной системы.
| LifeStep[a_List] := MapThread[If[(#1 == 1 && #2 == 4) || #2 == 3, 1, 0]&, {a, Sum[RotateLeft[a, {i, j}], {i, -1, 1}, {j, -1, 1}]}, 2] |
А это пример оптимизированной программы, которая оперирует сосписками живых клеток.
| LifeStep[list_] := With[{u=Split[Sort[Flatten[Outer[Plus,list,N9,1] ,1]]]}, Union[Cases[u,{x_,_,_}->x], Intersection[Cases [u,{x_,_,_,_}->x],list]]] N9=Flatten[Array[List,{3, 3},-1], 1] ; |
Система Mathematica позволяет легко создавать программы, состоящие из нескольких компонент.
Здесь приведены составляющие программы, моделирующей поведение клеточных систем
| CenterList[n_Integer]:=ReplacePart[Table[0, {n}], 1, Ceiling[n/2]] ElementaryRule [num_Integer] := IntegerDigits[num, 2, 8] CAStep[rule_List, a_List] :=rule[[ 8 - (RotateLeft[a] + 2 (a + 2 RotateRight[a])) ]] CAEvolveList[rule_List, init_List, t_Integer] :=NestList[CAStep[rule, #]&, init, t] CAGraphics[history_List] :=Graphics[Raster[1 - Reverse[history]], AspectRatio -> Automatic] |
Пример работы программы.
Show[CAGraphics[ CAEvolveList[ElementaryRule[30], CenterList[101], 50]] ];
 |
Mathematica имеет компилятор для оптимизации программ, которые работают со списками и числами.
| CAStep = Compile[{{rule, _Integer, 1}, {a, _Integer,1}}, rule[[ 8 - (RotateLeft[a] + 2 (a + 2 RotateRight[a])) ]]] |
Программы системы Mathematica зачастую являются прямой трансляцией теоретических положений справочной литературы.
Здесь вводятся необходимые определения для расчета импеданса электрической цепи.
 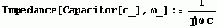 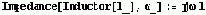   |
Использование данных выше определений.
 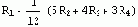 |
Пример электрической схемы, заданной при помощи символической спецификации.
 |
