Встроенные функции системы Mathematica
Использование предыдущего результата для построения графиков функций, задающих собственные значения, в зависимости от параметра.
Plot[Evaluate[v], {b, -10, 10}]
 |
Вы можете найти значение b, при котором первое собственное значение равно нулю...
Solve[First[v] == 0, b]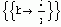 |
или найти интеграл от 0 до с от функции, задающей первое собственное значение.
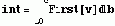  |
Теперь можно найти частичную сумму ряда Тейлора функции, являющейся результатом предыдущего интегрирования.
Series[%, {c, 0, 5}] |
Численное нахождение корня уравнения на заданном отрезке.
| FindRoot[int==1+c,{c,1}]{c->-0.554408} |
Простота работаты с формулами также важна при обработке данных.
Создание списка первых сорока простых чисел.
| Table[Prime[i], {i, 40}]{2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61, 67,71,73,79,83,89,97,101,103,107,109,113,127,131,137, 139,149,151,157,163,167,173} |
Приближение аппроксимирующей функцией.
| Fit[%, {Log[x],x,x2}, x]3.91287769352273429 x+0.0244902554054522703 x2-5.98809188219891908 Log[x] |
Вычисление суммы первых сорока простых чисел с применением аппроксимирующей функции.
| Sum[%, {x, 1, 40}]3090.16 |
Тот же результат, полученный точно.
| Sum[Prime[i],{i,1,40}]3087 |
Следующая команда объединяет в себе предыдущие и строит график разности между точными и приближенными значениями сумм простых чисел в зависимости от количества слагаемых.
  |
| Предыдущая глава | Оглавление | Следующая глава |
